Tema 33: Tallene fra 11 til 20: Subtraksjon med tierovergang (små trekk)
Mål
Hovedmål:
- Forklare hvilken subtraksjonsstrategi som er mest effektiv: gå om tieren, små trekk eller store trekk (telle opp eller ned).
Fokus
Denne og neste uke jobber elevene med subtraksjon med tierovergang. Dette er det siste temaet innenfor kompetansemålet «Tall» dette året. Tierovergang er veldig vanskelig for mange elever på 1. trinn, og ikke alle kommer til å mestre dette i år. På 2. trinn er derfor de 9 første ukene satt av til en repetisjon av det elevene har jobbet med i år.
Du kan med fordel tenke denne og neste uke under ett, og bruke god tid og flere økter på introduksjonen beskrevet nedenfor. Det viktigste disse to ukene blir altså å jobbe godt med forståelsen av tierovergang. Bruk god tid med elevene på samtale og utforsking, og ikke la ukesmålene eller Mattestreker-boka være førende for progresjonen. Gå videre med elevene når de selv er klare for det.
Som alltid er det viktig å bruke et rikt utvalg ev konkreter når man jobber med tallforståelse. I tillegg til noomstavene og fingrene bruker vi flere digitale konkreter i øvingslabbene sånn som Mengdelinjen og Noommodell. Det kan også være lurt å bruke noomene i øvingslabben Tallrepresentasjoner, og andre konkreter som man har brukt i egen undervisning tidligere.
Det er også fine samtalebilder i Mattesnakk-boka som det er lurt å bruke god tid på. Gjør gjerne dette etter at alle gruppene har vært gjennom introduksjonen beskrevet nedenfor.
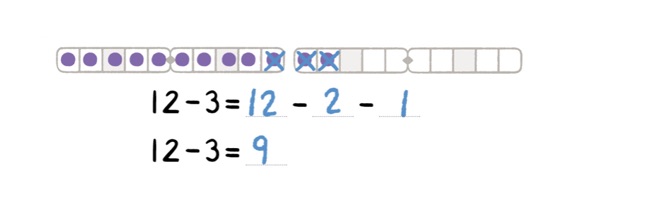
Vi deler også denne gangen subtraksjon inn i små og store trekk. For en repetisjon av hva dette er, så kan du lese temateksten til uke 22 hvor dette står utførlig beskrevet. Denne uken jobber vi med små trekk, og neste uke jobber vi med store trekk. Små trekk er den «vanlige» strategien der vi trekker fra toppen på denne måten:
For å introdusere subtraksjon med tierovergang er det fint å starte med å la elevene selv oppdage hva det faktisk er og hvorfor vi trenger det. Det beste er å gjøre dette gruppevis. Del klassen opp i for eksempel grupper av 4-6 elever, og jobb med én og én gruppe om gangen. La de andre elevene for eksempel gjøre ferdig ting på nettbrettet de ikke er blitt ferdige med, spille Numbers eller Big Numbers, leke med noomene eller spille brettspill/kortspill/terningspill. Du kan også utforme dette som stasjonsundervisning.
I den gruppen du jobber med:
La elevene for eksempel få utdelt en 10-er noomstav og en 2-er noomstav. Hvilket tall er dette?
La de så få oppgaven 12 - 2. Hva blir det?
Sett 12 tilbake igjen og gi så oppgaven 12-3. Hva blir dette? De vil selv oppdage at dette blir annerledes. Ha en samtale med elevene der de kommer med forslag til hvordan dette kan løses. Kom gjerne frem til at 3 kan deles i 2 og 1, slik at man først tar vekk 2 for å få 10, og deretter 1 fra 10-eren. Knytt dette sammen med tiervennene.
Gjenta dette med flere oppgaver som for eksempel 12 - 4, 12 – 5, 11-2, 11-3 og/eller 13-5.
Gå deretter over til oppgaver på fingrene.
To av elevene viser et tall mellom 11 og 19 (den ene eleven viser 10 og den andre eleven viser for eksempel 4). Nå skal man ta bort for eksempel 6. Ha en samtale om hvordan dette kan løses. Det er fint å slutt komme frem til samme strategi som ovenfor: Man kan først ta vekk de 4 fingrene som er alene, og deretter ta vekk 2 fra de ti fingrene. Fortsett med dette til elevene mestrer det.
For at alle elevene skal få en forståelse av hva subtraksjon med tierovergang er, så vil mange av elevene trenge å gjenta denne øvelsen mange ganger over flere økter. Du kan med fordel gjøre følgende steg:
Gjøre denne introduksjonen én gang med alle gruppene.
La alle elevene få prøve seg på de første sidene i Mattestreker. (På denne måten bygger du opp det egne initiativet hos elevene for å forstå subtraksjon med tierovergang.)
Ha en samtale om bildene i Mattesnakk-boka og jobbe litt med de digitale verktøyene.
Gjøre denne introduksjonen gruppevis igjen med de elevene som trenger det. De elevene som raskt får dette til kan jobbe på egenhånd i Mattestreker, på nettbrettet og på kopiark. På den måten får du den ekstra tiden du trenger til de elevene som må ha mange repetisjoner.
Du kan gjenta denne rekkefølgen flere runder, til alle elevene har en grunnleggende forståelse av hva tierovergang er (selv om de av ulike grunner ikke kommer frem til helt riktig svar).
I økt 1 i Mattetreker jobber elevene med tierovergang ved hjelp av mengdelinjen. Husk at det viktigste er at elevene får en forståelse av hva subtraksjon med tierovergang er, ikke at de får riktig svar på oppgavene. Den første oppgaven er en tankenøtt for å finne en ukjent del. Denne oppgaven ligger også tilgjengelig som smartboard-bilde som du finner under økten.Det er lurt å først gjøre oppgaven som en samtale i plenum, før elevene gjentar den samme oppgaven individuelt i boka.
I økt 2 i Mattetreker jobber elevene først med tierovergang ved hjelp av mengdelinjen, og deretter med rene talluttrykk. Elevene kan gjerne ha noomstaver tilgjengelig som de på eget initiativ kan finne frem og bruke mens de regner.
I økt 3 i Mattetreker jobber elevene med regnefortellinger og modellering. Bildene fra boka ligger også som Smartbord-bilder på økta. Det er lurt å først gjøre oppgavene som en samtale i plenum, før elevene gjentar de samme oppgavene individuelt i boka.
Den rike oppgaven i økt 4 er igjen spillet Tallfantasi som elevene har gjort før. Men denne gangen består kortene av subtraksjonsoppgaver uten tierovergang.
Lurt å Vite
Hjemmelekse
 Skriv Ut
Skriv Ut
Økt 1: Subtraksjon med tierovergang: Små trekk
Mål
Elevene skal kunne:
Gå om tieren når de subtraherer med tierovergang.
Vise at de bruker "telle ned" strategien når de subtraherer små tall (små trekk).
Ekstra utstyr
Fokus
Beskrivelse
Økt 2: Subtraksjon med tierovergang: Små trekk
Mål
Elevene skal kunne:
- Vise at de bruker «telle-opp» strategien når de subtraherer store tall (store trekk).
Ekstra utstyr
Fokus
Beskrivelse
Økt 3: Subtraksjon med tierovergang: Sammenlikning
Mål
Elevene skal kunne:
- Lage enkel regnefortelling med subtraksjon med tierovergang, med støtte i bilde og modell (tallvenner).
Ekstra utstyr
Fokus
Beskrivelse
Økt 4: Rik oppgave: Titallsfantasi – subtraksjon uten tierovergang
Mål
Eleven kan subtrahere tall uten tierovergang opp til 19.
Ekstra utstyr
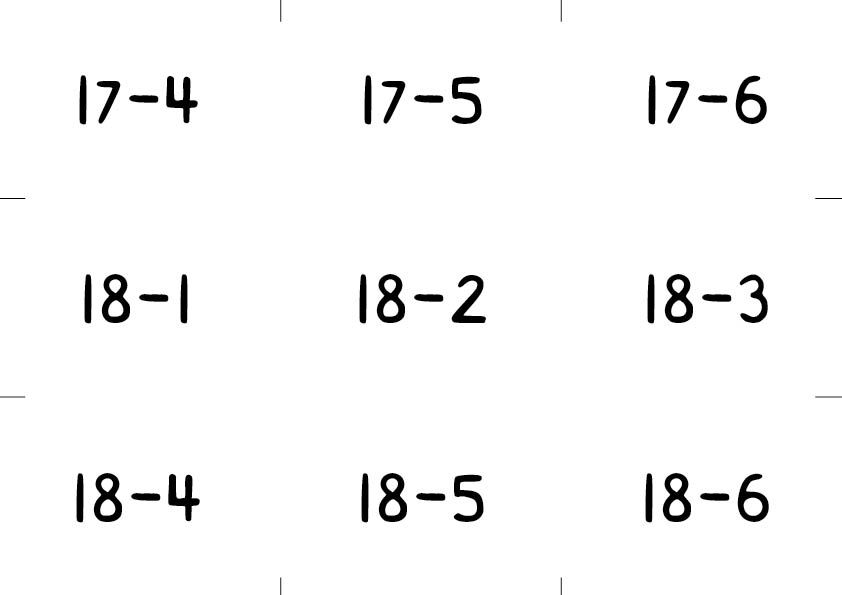
Tallkortene som du finner til høyre. Tallkortene klippes opp, og hver gruppe med 4 elever får ett sett hver. Det kan være lurt å printe tallkortene på tykkere papir eller lime et ekstra ark bak på tallkortene slik at det ikke er mulig å se tallene gjennom arket.
Noomstaver. Fordel noomstavene jevnt slik at alle gruppene har så mange noomstaver som mulig.
Skrivesaker.
Fokus
Beskrivelse
Her kommer først en kort beskrivelse. For en utfyllende beskrivelse klikk i den gule boksen til høyre.
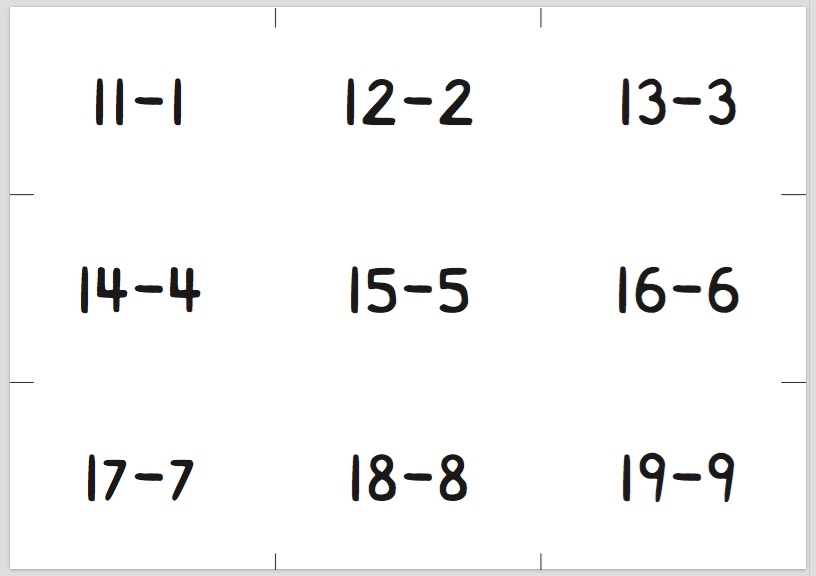
Dette er samme spillet som i den rike oppgaven i økt 24.4, 28.4 og 32.4, men nå er det subtraksjonsoppgaver uten tierovergang på kortene. Hvis en elev for eksempel trekker kortet 13-2, så skal eleven selv _finne ut hva svaret blir _ og deretter formidle dette. Riktig svar på oppgaven blir dermed 11.
Fra teksten til økt 24.4:
«Dette er et spill som er inspirert av spillet Fantasi, og tallkortene er spillkort. Elevene deles i grupper på 4 elever i hver gruppe.
Elevene skal etter tur trekke et kort, og deretter forklare for de andre på laget hvilket tall som står på kortet. Men pass på: Det er ikke lov å si hvilket tall det er eller tegne tallsymboler!
For å forklare tallet kan elevene bruke noomstaver, tegning (de kan tegne noomer eller andre mengder, men ikke skrive tall), fingre eller annet de kommer på.»
 Rik oppgave: Titallsfantasi – subtraksjon uten tierovergang
Rik oppgave: Titallsfantasi – subtraksjon uten tierovergang


Denne beskrivelsen er den samme som i økt 24.4.
Siden elevene kan vise oppgaven med noomer, kan de også bruke disse som en hjelp til å finne svaret. Det gjør det enklere for alle elevene å få til oppgavene. Men husk at det er selve svaret som den andre eleven skal gjette riktig, ikke regnestykket.
TIPS: Det første arket er enklere enn de andre. Det kan være en god ide å først starte med kortene på dette arket, eller nivådele gruppene og la noen av gruppene starte med dette arket.
Introduksjon av oppgaven:
Elevene deles først i par. Deretter går to og to par sammen slik at hele klassen er delt i grupper på 4.
Elevene i ett elevpar er på samme lag, og sammen spiller de mot det andre elevparet på gruppen sin.
Gruppene får utdelt tallkort, noomstaver og skrivesaker.
Tallkortene legges i en bunke med tallene vendt ned mot pulten.
Slik er spillets gang:
La oss si at det er elevpar 1 sin tur.
- Først av alt startes tiden. Tiden er 60 sekunder. Enten kan læreren ta tiden, eller så kan elevene selv ta tiden ved å bruke klokka på nettbrettet.
Elev 1 i elevpar 1 trekker et tallkort som den ikke viser til noen.
Eleven skal nå beskrive tallet/"svaret" til andre eleven i paret sitt (elev 2 i elevpar 1).
Eleven kan bruke både noomstaver, tegne mengder, bruke fingre eller si feks "en tier og to enere " for å beskrive 12. Men OBS: Elev 1 har ikke lov til å si hvilket tall det er eller skrive selve tallet.
Elev 2 i elevpar 1 prøver å gjette hvilket tall det er.
Så fort elev 2 har gjettet riktig, trekker elev 1 et nytt tallkort.
Slik fortsetter spillet helt til de 60 sekundene er brukt opp. Da skriver elevparet ned hvor mange poeng de fikk denne runden. Hvert riktige svar gir 1 poeng.
- Deretter er det elevpar 2 sin tur. Klokka startes for å telle ned 60 sekunder, og elev 1 i elevpar to trekker et kort. Deretter fortsetter spillet med punktene over.
Når det er elevpar 1 sin tur igjen, så byttes rollene. Nå er det elev 2 som skal trekke kort mens det er elev 1 som gjetter.
På denne måten bytter elevene i begge elevparene på å trekke kort og gjette, runde for runde.
Vinneren av spillet er den som har flest poeng etter et forhåndsbestemt antall runder (feks 4 runder på hvert elevpar, som er det samme som at hver elev i gruppen får trekke kort to runder hver).
Deretter kan man for eksempel bytte grupper, og spille en gang til.
Lav inngangsterskel:
Ta frem en elev og spill spillet sammen med denne eleven, mens du forklarer regler og de andre elevene ser på.
Ta så frem 4 elever, del dem i to grupper, og la dem spille et par runder mens de andre ser på. Vis hvordan man kan telle ned tid på nettbrettet.
Neste nivå:
Del elevene inn i elevpar og sett deretter sammen to og to par sammen slik at hele klassen er delt i grupper på 4.
Du kan også la elevene selv velge hvilket elevpar de vil konkurrere om.
Del ut tallkortene, noomstaver og tegnesaker. Leg tallkortene i en bunke med tallene vendt ned mot pulten.
Gjør klar nettbrettene til tidtaking, og sett deretter i gang spillet.
Åpen utgang:
- La elevene lage tallkort selv! De kan lage regnestykker med så høye tall de vil, og inkludere brøker og desimaltall om de mestrer dette eller har lyst til å teste det ut. Utfordringene er uendelig.