Mål

Elevene skal kunne:

• Skrive likhetstegn og gjøre to ulike mengder med forskjellig representasjonsform (noomer og tall) like.
• Benytte relasjonstegn, og sammenligne to ulike mengder med forskjellig representasjonsform (noomer, tall).
• Sammenligne to selvvalgte mengder under 5, og benytte riktig relasjonstegn.

Fokus

Denne uka skal elevene lære om relasjonstegnene =, <, >. Du kan lese mer om ulike måter barn forstår disse tegnene på under "lurt å vite" lengre ned på siden.

I økt 1 jobber elevene med "=". Med noomer og tall skal elevene gjøre begge sidene av ligningene like hverandre. Husk at vi ennå ikke har begynt med "+" og "-", men bruk gjerne både ordene "pluss" og "minus" muntlig.

I økt 2 introduseres elevene for "=, <, >". I Mattestreker skal de kunne fylle inn tegnene i uttrykk med noomer og tall.

I økt 3 er relasjonstegnene allerede fyllt inn, og elevene skal fylle inn tall og noomer slik at likhetene og ulikhetene stemmer (som i økt 1 bare nå med alle relasjonstegnene).

Den rike oppgaven i økt 4 handler også om relasjonstegn. Elevene skal jobbe i par tegne relasjonstegn og bruke terninger og noomer.

Lurt å Vite

Relasjonstegnene =, <, >

Tegnene ”=, <, >” kalles i matematikk for relasjonstegn. Navnet har de fått fordi de representerer en relasjon/sammenheng mellom den venstre og den høyre siden:

• 3 + 1 = 4: Her er venstre og høyre side like.

• 3 + 1 < 5: Her er venstre siden mindre enn høyre side.

• 3 + 1 > 2: Her er venstre siden større enn høyre side.

Å forstå tegnene =, <, > som relasjonstegn er en algebraisk (eller syntaktisk) måte å forstå tegnene på.

Den andre måten å forstå tegnene =, <, > på kalles aritmetisk (eller semantisk). Da forstå man for eksempel ”=” som ”å gjøre en utregning” eller ”svaret”.

Skolen har en lang tradisjon for å først introdusere ”=” på en aritmetisk måte (finne ”svaret”) og deretter bygge videre på denne aritmetiske forståelsen når elevene skal lære algebra. Årsaken til dette stammer fra den kjente psykologen Jean Piaget, som argumenterte for at barn ikke vil være i stand til å tenke så abstrakt som algebra krever før i 12-års alderen (se lengre ned for å lese mer om dette).

Andre argumenterer for at algebraiske tankemåter kan introduseres allerede fra skoleststart, og at mangelen på dette kan være med på å utvikle matematikkvansker (se lengre ned for å lese mer om dette).

I DragonBox Skole har vi valgt å legge oss på en gylden middelvei:

• Når vi introduserer relasjonstegnene i dette kapittelet så gjør vi det på en algebraisk måte for at elevene skal ha møtt denne tankegangen.

• Når vi introduserer addisjon og subtraksjon holder vi oss utelukkende til den aritmetiske måten.

• I de rike oppgavene vil elevene møte algebraiske måter å tenke på, med da innen det man kaller ”Early Algebra” som er beregnet for så unge elever (se lengre ned for å lese mer om dette).

UTFYLLENDE KOMMENTARER TIL TEKSTEN OVER:

• Piaget snakket om fire stadier for kognitiv utvikling:
• det sansemotoriske stadiet.
• det pre-operasjonelle stadiet.
• det konkret-operasjonelle stadiet.

• det formelt-operasjonelle stadiet. Det siste stadiet er det man tradisjonelt har ment elevene må ha nådd før de kan begynne med algebra. Man har tidligere tenkt at dette oppnås i 12-års alderen, men mange nyere studier viser at dette ikke oppnås før mye senere.

• Noen av dem som argumenterer mot Piaget er blant annet Johan Mason med flere i boka Developing Thinking in Algebra. Et av argumentene er at barn har lært et språk før de begynner på skolen, og det å lære et språk krever et abstrakt konsept. Man kan derfor kan gå ut ifra at elever helt ned i barneskolen er mestere i abstraksjon og ergo vil har mulighet til å tilegne seg algebraisk tankegang. Det er da viktig å presisere at man ikke tenker algebra slik det undervises på ungdomskolen, men det som kalles ”Early Algebra”. Denne masteroppgaven skrevet av Øystein Krovik tar for seg noen av disse argumentene på en oversiktlig måte.

• Early Algebra handler om å få elevene til å se sammenhenger som gjelder for alle tall. Et eksempel er kommutativitet som vi skrev om i ukestema 4 (2 + 3 er det samme som 3 + 2). Et annet eksempel er at hvis man adderer med et tall og subtraherer med det samme tallet så går det "opp i opp" (feks 10 + 3 - 3 = 10). Her kan du lese mer om Early Algebra.

Hjemmelekse

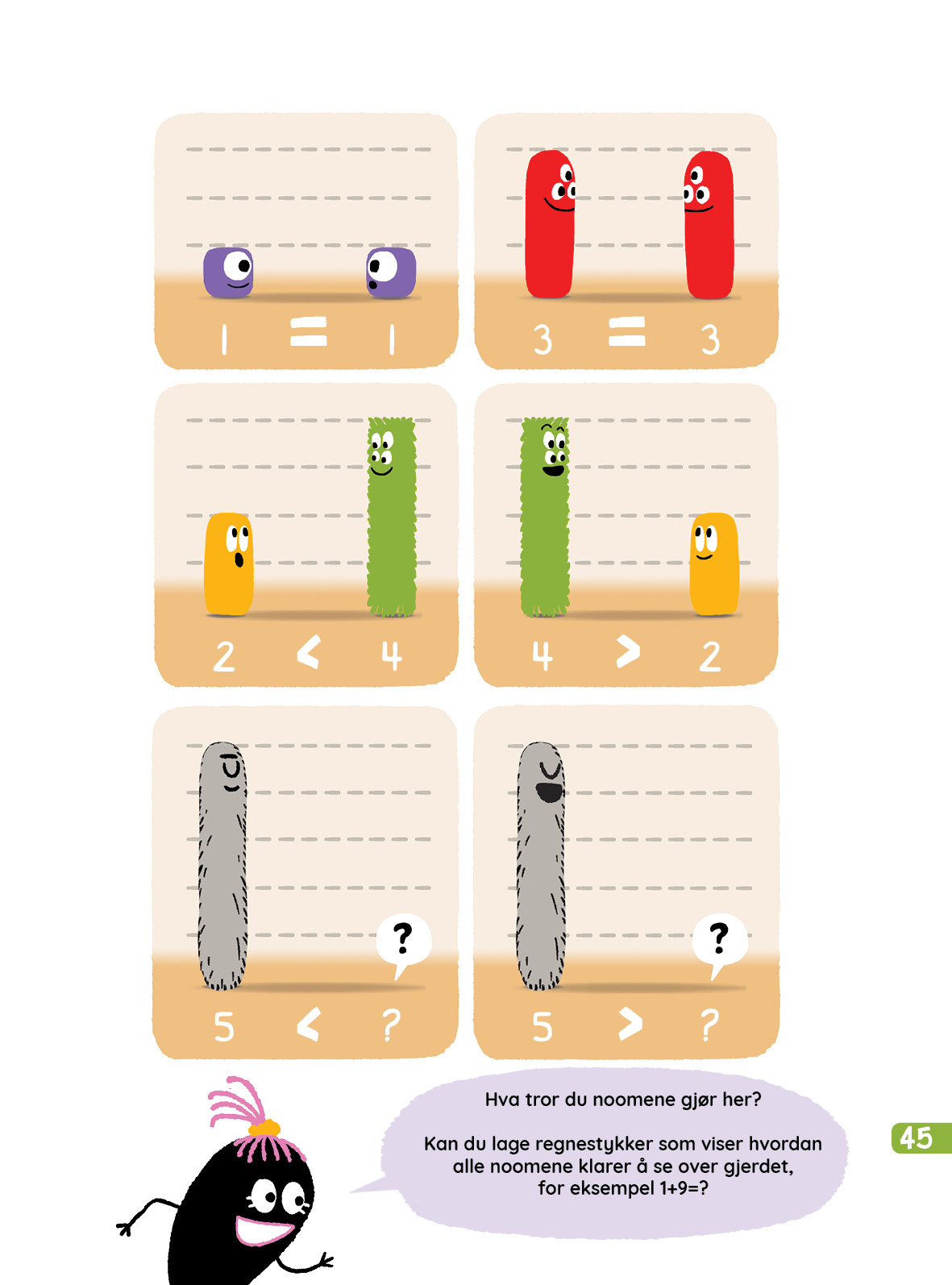
Denne uka er vårt forslag til lekser å igjen oppmuntre til en matematikk-dialog mellom elever og foreldre. Mattesnakk side 46-47 (om likhet) og side 45 (om likhet og ulikhet) passer bra til dette denne uka.

Som tidligere kan man også bruke følgende som lekser:

• Mattestreker er fin å gi som lekse hvis det er sider der de ikke rekker på skolen. De som er ferdige med alt kan enten få kopiark eller nettbrettet med seg hjem.

Som beskrevet i forrige uke anbefaler vi i så fall at du bruker de siste minuttene av timen til å gå gjennom alle oppgavene muntlig sammen med elevene (fortrinnsvis i samling). På denne måten blir oppgavene en slags repetisjon for elevene istedenfor at det føles som helt nytt stoff.

• Nettbrettene er fine å sende hjem som lekse. På nettbrettet kan de enten gjøre ferdig aktivitetene som hører til øktene denne uka, eller de kan spille DragonBox Numbers eller andre spill.

Som beskrevet i forrige uke kan det være lurt å la laderne være igjen på skolen. Et tips er da å innarbeide en fast rutine med at elevene setter nettbrettene til lading hver morgen og deretter legger de i sekken når dagen er over.