Mål

Hovedmål:

• Forklare verdien av myntene vi bruker (1-kroning og 5-kroning), og benytte dem i kjøp- og salgssituasjoner.

Fokus

Denne uka introduseres elevene litt mer grundig for mynter, penger og verdi. Det er to hovedfokus:

• Å forstå verdien av myntene.

• Å forstå at varer også har en verdi på lik linje med penger, og at den samlede summen av varer og penger gir noe vi har valgt å kalle "min formue" eller "verdien av det jeg har".

Det nederste av disse to punktene leder opp mot kjøp, salg og veksling. Målet er å få elevene til å forstå at verdien man har med seg inn i butikken er den samme som verdien man har med seg ut av butikken. Og det samme, verdiene som er i butikken før salget er de samme som verdiene som er i butikken etter salget.

I økt 1 jobber elevene med å summere enten penger eller verdien av flere varer. Dette er første steget på veien for å forstå kjøps- og salgssituasjoner.

I økt 2 jobber elevene med å kunne summere verdien av både penger og varer sammen. Dette er andre steget på veien for å forstå kjøps- og salgssituasjoner.

Veksling handler nettopp om å forstå at verdien av varene og pengene man har etter at man har handlet, skal være den samme som verdien av pengene man hadde før man handlet. En utfordring for noen av elevene vil være å forstå at varene kan "omformes" til penger – de har en pengeverdi.

I økt 2 foreslår vi å bruke øvingslabben Sammenligning. Man kan da ha penger på den ene siden, og penger + varer på den andre siden, og målet er selvfølgelig at det skal være likt mellom de to sidene. Likhet mellom sidene betyr at verdien av det man hadde med seg inn i butikken (venstre side) er den samme som verdien at det man har med seg ut av butikken (høyre side). Et tips er å bruke røntgenmaskinen over presangene. Da får man sett presangenes verdi i kroner.

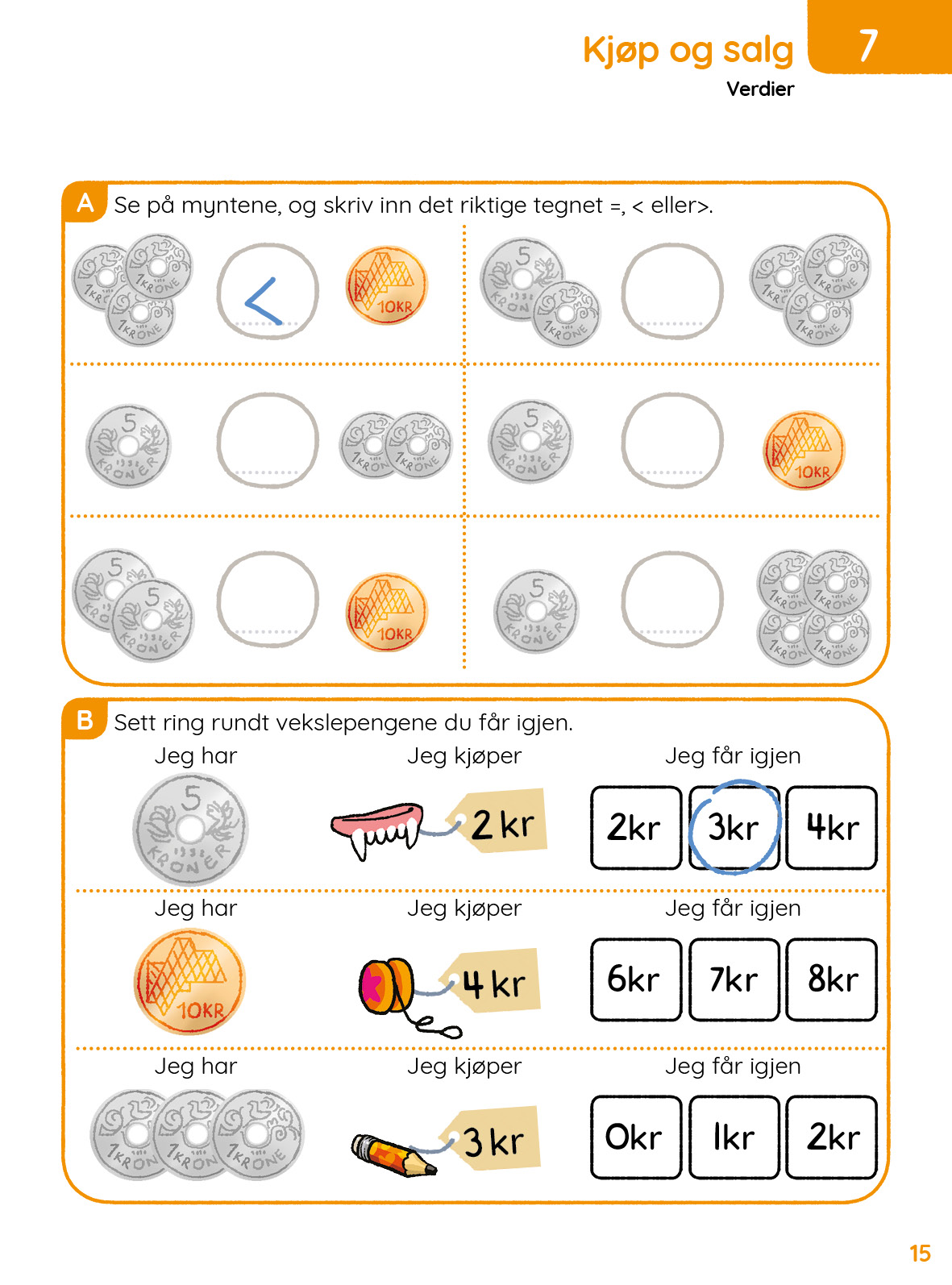
I økt 3 jobber elevene med konkrete kjøps- og salgssituasjoner hvor temaet er å gi igjen veksel. Det er en Vekslings-øvingslabb og også fine quizer med veksling som elevene kan prøve seg på. Før de begynner å jobbe i boka så ligger det et bilde man kan bruke på Smartboarden. Bildet er av samme typen som de oppgavene elevene møter i Mattestreker. Det kan være lurt å gå gjennom dette bildet på Smartboarden før elevene prøver seg på egen hånd.

Den rike oppgaven i økt 4 handler også om penger, og målet er å lage en spareplan som skal følge gitte regler.

Lurt å Vite

Hjemmelekse