< Tilbake

Tema 20: Tallene fra 6 til 9: Subtraksjon med 5 som base

Mål

Hovedmål:

Forklare hvordan subtraksjon kan handle om å ta vekk noe, eller å finne forskjellen mellom noe.

Fokus

Denne uka er temaet noe av det samme som i uke 13 og 17 (5 + x), men denne gangen er temaet subtraksjon. Elevene skal jobbe subtraksjon i området 6-9, hvor man enten trekker fra 5 eller hvor svaret blir 5. Typiske oppgaver er:

6 – 1 =
6 – 5 =
7 – 2 =
7 – 5 =

og så videre.

På samme måte som tidligere jobber elevene på følgende måte:

Noomer (kutte av), noommodell (sammenligne med usynlig noom) og sammenhengen mellom disse.
Tallvennemodell.
Enkelboksen.
Andre represenatsjoner som fingre.
Noomodell og tallvennemodell sammen med bilder og likninger.

Elevene får modellene som er knyttet opp mot konkreter (noomene eller øvingslabber). Etterpå jobber man med sammenhengene mellom modellene, og disse settes så sammen med bilder (matematisk modellering) og talluttrykk.

I økt 1 jobber elevene med støtte i noomer og noommodell. Oppgavedel A handler om hva som skjer når man kutter av noomer, men oppgavedel B handler om hva som skjer når man sammenligner noomer (noommodell). I oppgavedel C trekkes de to sammen, og elevene skal se sammenhengen mellom å kutte av og å sammenligne. Det kan virke ganske intuitivt for oss voksne, men noen elever forstår ikke dette av seg selv. Det er derfor viktig å jobbe godt denne sammenhengen slik at alle elevene forstår dette.

I økt 2 jobber elevene med tallvennemodellen, enkelboksen og fingre.

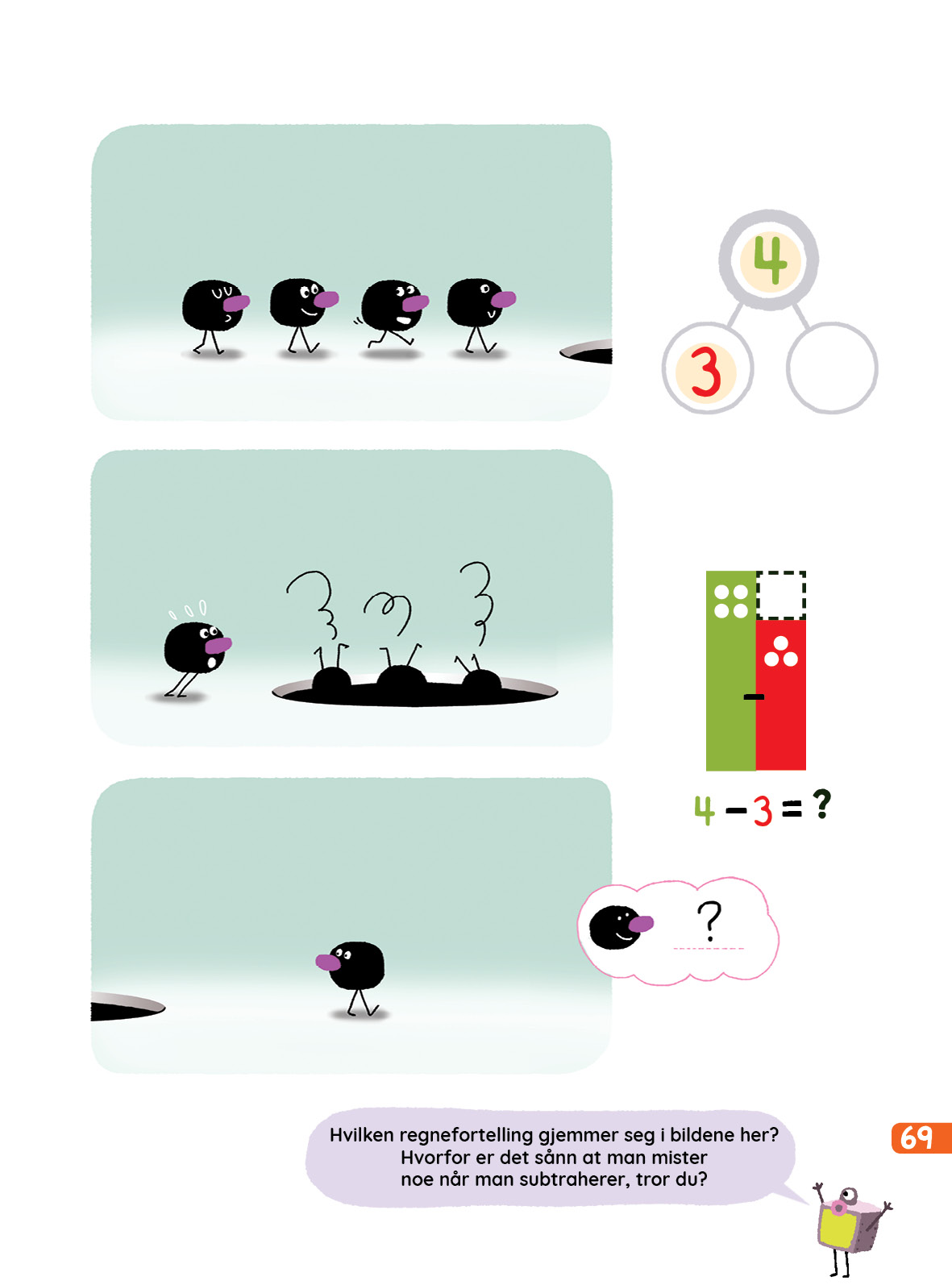
I økt 3 jobber elevene med tallvennemodell og noommodell sammen med bilder og talluttrykk. Når elevene skal på en konkret situasjon (i dette tilfellet et bilde) og deretter knytte en modell til bildet, kalles dette matematisk modellering. Denne økten er det også 4 ekstra bilder til Smartboarden, lignende de som er i Mattestreker. Disse er fine snakke om i plenum sammen med elevene før de begynner å jobbe i boka. La elevene selv prøve å finne ut hva som er spørsmålet i bildet, og la dem deretter prøve å lage en noommodell og en tallvennemodell som passer til bildet.

I den rike oppgaven i økt 4 skal elevene bruke noomene til å lage subtraksjonsstykker.

Skriv Ut

Økt:

Ukas Øvingslab’er:

Tallrepresentasjoner

Tallvenner

Mengdelinje

Noom modell: avansert

Tema 20: Tallene fra 6 til 9: Subtraksjon med 5 som base

Økt 1: Tallene fra 6 til 9: Subtraksjon med noomer

Mål

Elevene skal kunne:

Dekomponere mengder under 10, med støtte i modell (noomer).

Mattesnakk: Tallene 6-9 med 5 som base

Tallrepresentasjoner: Med tall, noomer, noommodell, enkelboks og usynlig noom.

Mattestreker del 2: Tallene fra 6 til 9: Subtraksjon med noomer

Butikk: 1 vare - Hvor mye har jeg igjen? (5)

Tallvenner: Under 10

Tallfakta: x-y=5 eller x-1

Likninger: Subtraksjon med noomer x-1 og x-5

Noom modell: modell til likning: Subtraksjon under 6

Tallskriving: 6 til 9

Puslespill: 10-venner

Butikk: 2 varer - Hvor mye har jeg igjen? (10)

Gardin: Likninger med enkelbokser eller fingre: x-5 eller x-1

Tallninja: Under 10

Gardin: Tell penger.: Under 10

< Tilbake