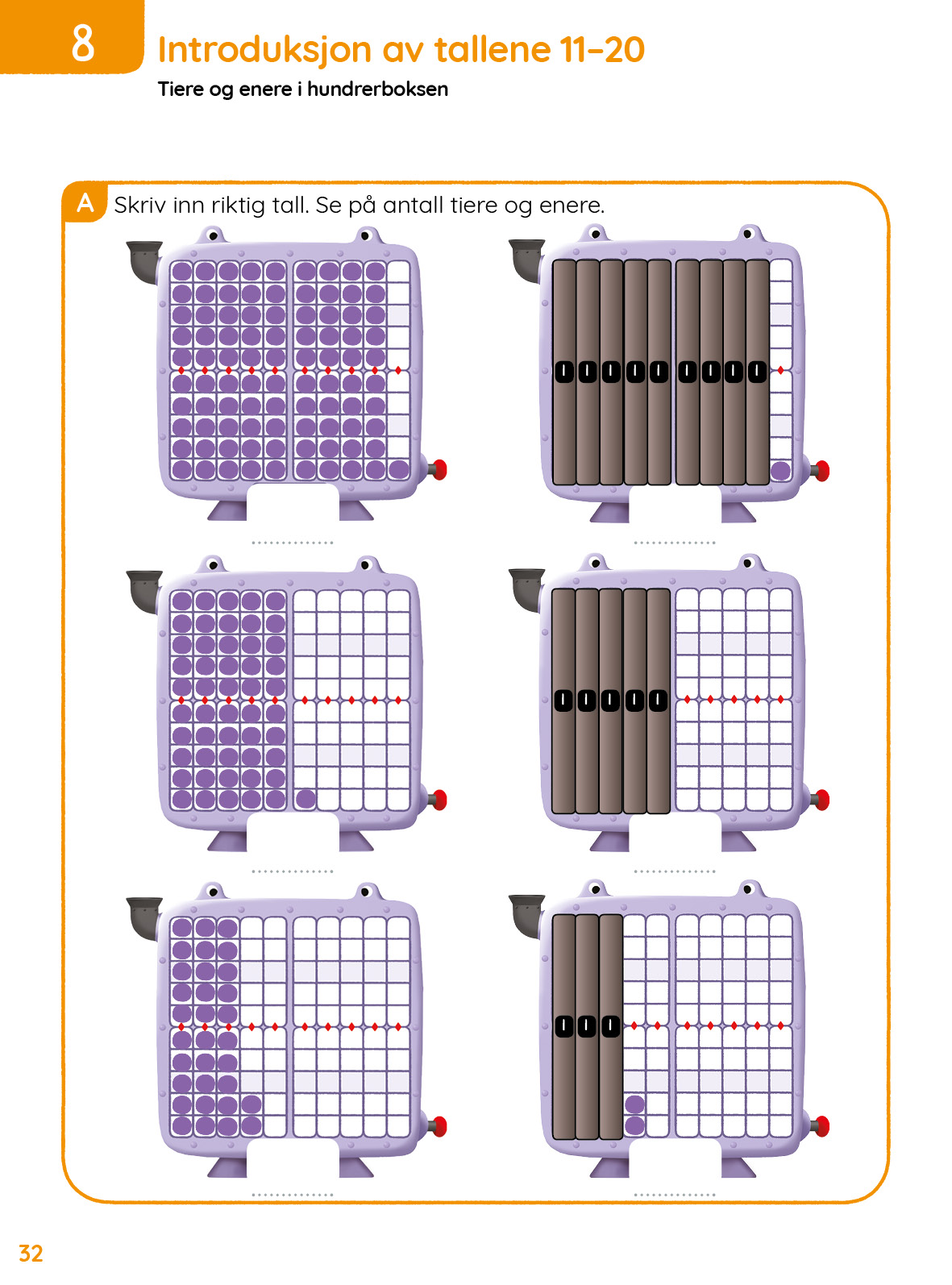
Tema 22: Tallene fra 6 til 9: Tallinjen og subtraksjonsstrategier
Mål
Hovedmål:
- Bruke hensiktsmessige strategier for å løse addisjons- og subtraksjonsoppgaver med tall under 10.
Fokus
Denne uka introduseres elevene for tallinjen. I øvingslabben er tallinjen loddrett, mens i Mattestreker er tallinjen vannrett slik som er vanlig.
I tillegg til tallinja møter elevene to forskjellige subtraksjonsstrategier:
”Trekke fra toppen” som man bruker ved små trekk.
”Trekke fra bunnen” som man bruker ved store trekk.
Hensikten med disse to strategien vil bli mer synlig når elevene jobber med høyere tall, så for å forklare disse to strategiene bruker jeg nå et eksempel med et høyt tall.
Små trekk betyr at man trekker fra noe lite. For eksempel i oppgaven
100 – 2 =
så er 2-tallet et lite tall, og dette er dermed subtraksjon med små trekk. Når man skal regne ut 100 – 2 så trekker man fra toppen. Det betyr at man begynner med hundre og tar bort 2 slik at man får 100, 99, 98.
Dette bildet viser et eksempel på små trekk fra Mattestreker:
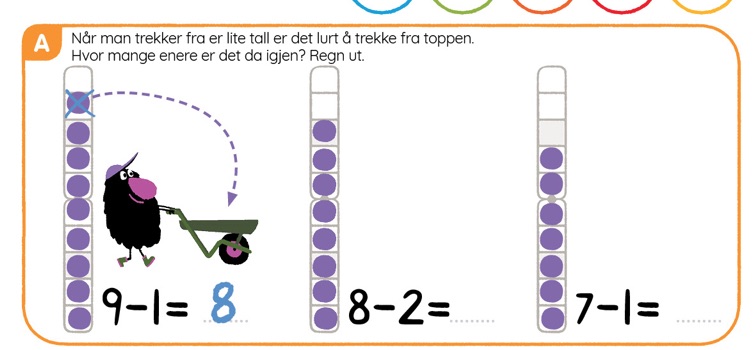
Store trekk og strategien vi bruker her er det som er litt forskjellig fra hvordan vi pleier å tenke om subtraksjon. Store trekk betyr at man trekker fra noe stort, for eksempel:
100 – 88 =
Her er 88 et stort tall i forhold til 100, og man har dermed subtraksjon med store trekk. De fleste bruker automatisk strategien ”trekke fra bunnen” når de skal trekke fra noe stort, men de færreste er bevisste på at de gjør det. For elevene sin del er denne bevisstgjøringen veldig viktig. Jeg skal nå forklare hva å ”trekke fra bunnen” betyr.
I oppgaven 100 – 88 så pleier vi ikke å starte på 100 og deretter telle oss nedover til 12. Istedenfor starter vi på 88 og teller oss oppover til 100. Dette er fordi 88 er nærmere 100 enn 0. Det vi egentlig gjør når vi teller oppover på denne måten, er å trekke vekk de nederste 88, slik at vi deretter står igjen med det som er mellom 88 og 100. Og det er disse vi teller når vi teller oppover. Altså vi trekker fra bunnen.
Dette bildet viser et eksempel på store trekk fra Mattestreker:
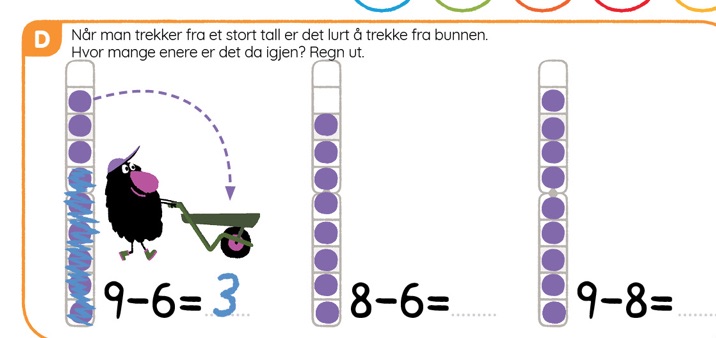
I økt 1 jobber elevene tallinjen. Det er en egen øvingslabb for dette.
I økt 2 jobber elevene subtraksjonsstrategier ved små og store trekk. Det er veldig fint å bruke øvingslabben Mengdelinje her. I den øvingslabben kan man selv velge om man vil trekke fra toppen eller trekke fra bunnen.
Økt 3 er en repetisjonsøkt for tallene under 10. Her møter elevene addisjon og subtraksjon med noomodell, tallvennemodell og talluttrykk. Det er også noen oppgaver med relasjonstegn i talluttrykk. Det kan være lurt å starte økten med en repetisjon av små og store trekk.
Den rike oppgaven i økt 4 handler om subtraksjon med noomene.
Lurt å Vite
Hjemmelekse
 Skriv Ut
Skriv Ut
Økt 1: Tallene fra 6 til 9: Tallinjen
Mål
Elevene skal kunne:
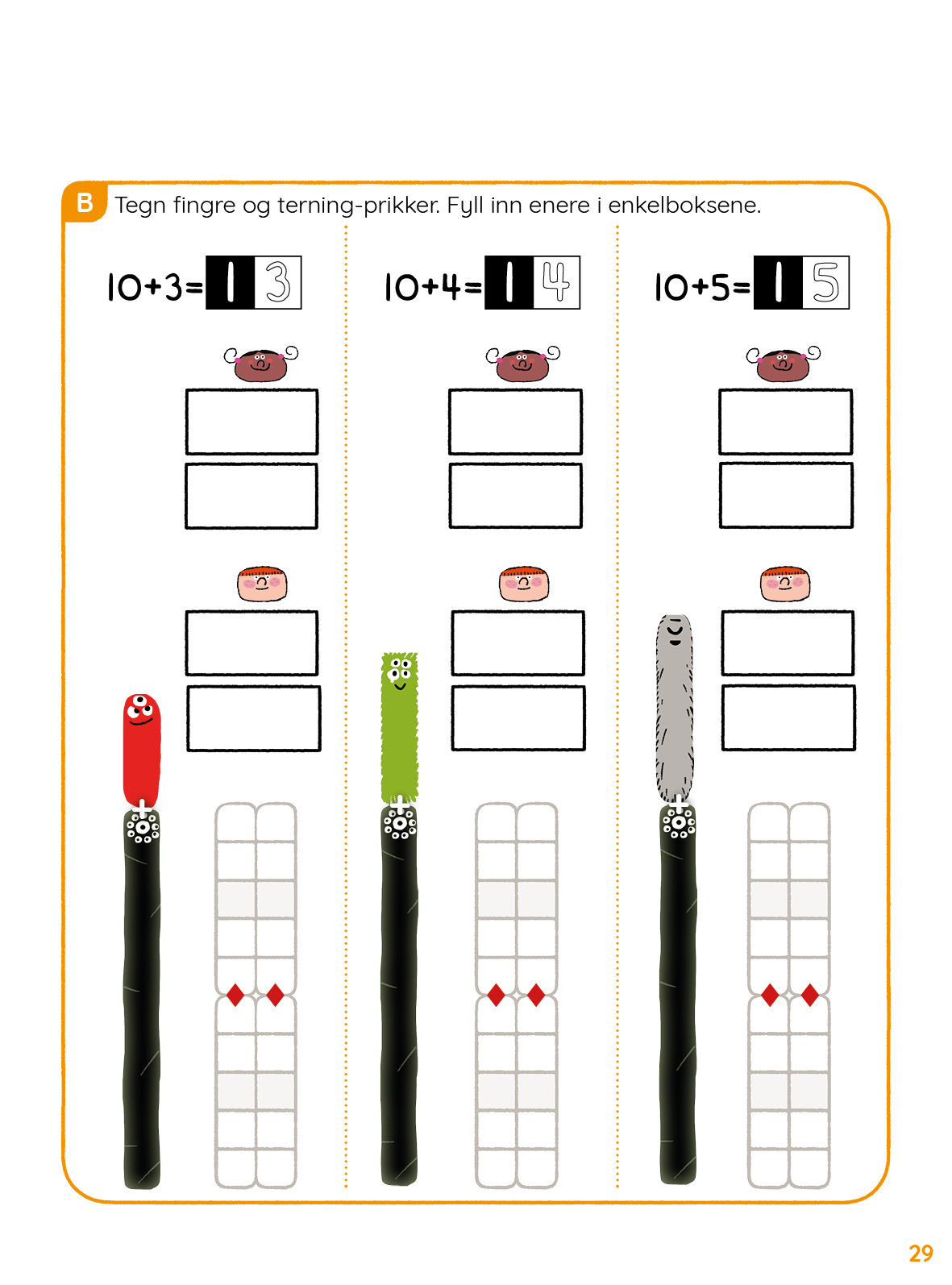
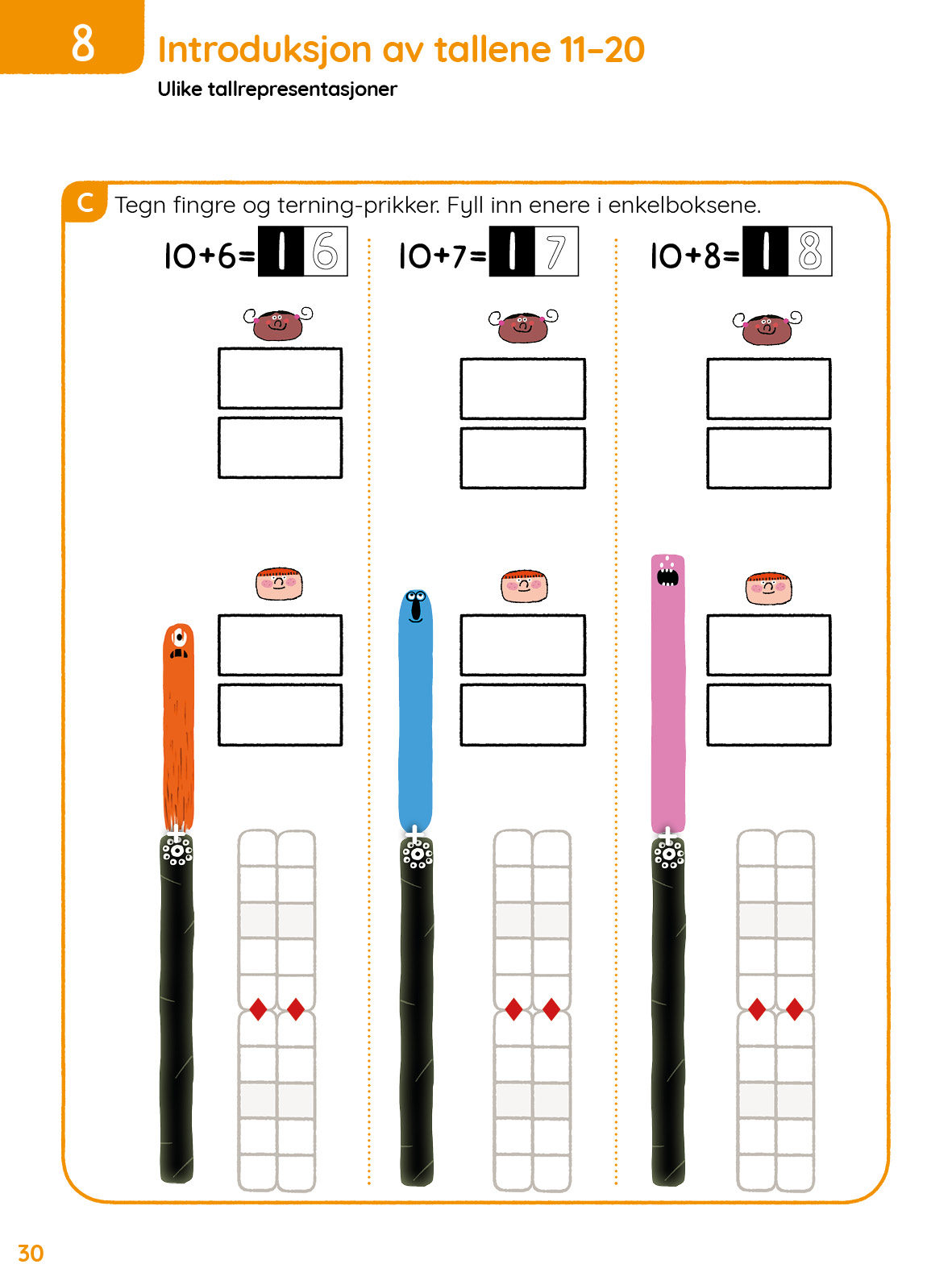
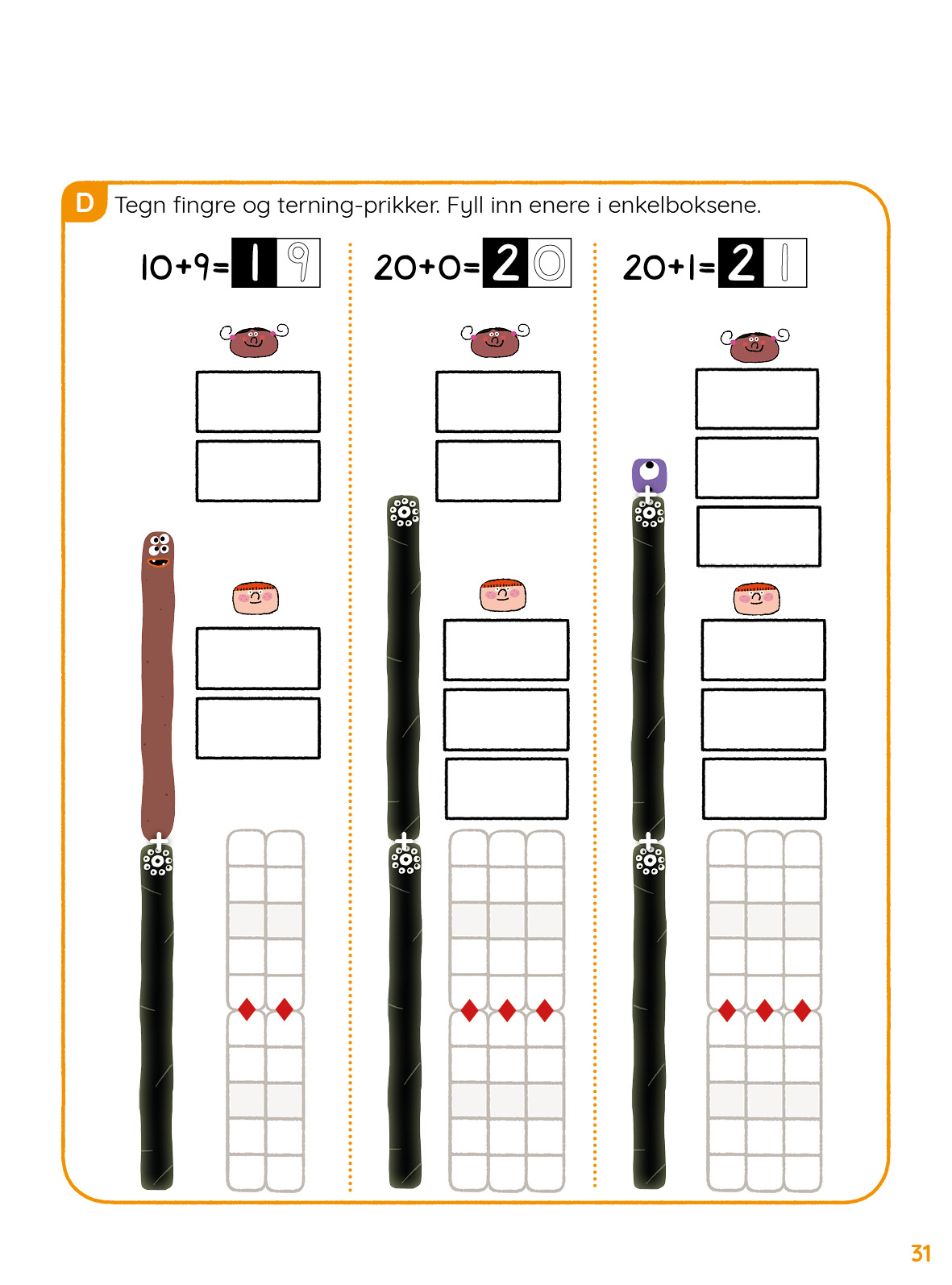
- Tolke ulike tallrepresentasjoner (noomer, penger, terninger, fingre) og plassere dem på tallinjen.
Ekstra utstyr
Fokus
Beskrivelse
Økt 2: Tallene fra 6 til 9: Subtraksjonsstrategi ved små og store trekk
Mål
Elevene skal kunne:
- Visualisere med fingrene hvilken subtraksjonsstrategi er mest effektiv ved små og store trekk (telle opp eller ned).
Ekstra utstyr
Fokus
Beskrivelse
Økt 3: Tallene fra 6 til 9: Repetisjon
Mål
Elevene skal kunne:
- Bruke hensiktsmessige strategier for å løse addisjons og subtraksjonsoppgaver med tall under 10.
Ekstra utstyr
Fokus
Beskrivelse
Økt 4: Rik oppgave: Subtraksjon med enkelbokser
Mål
Elevene kan subtrahere med tallene opp til 9, og de kan lage egne subtraksjonstykker.
Ekstra utstyr
Brikker, 45 stk til hvert elevpar. Her kan man bruke tellebrikker, noomer, makaroni, steiner, skjell eller hva som helst. Det eneste som er viktig å huske på er at brikkene ikke må være større enn rutene i enkelboksene.
Kopier av enkelbokser. Hvert elevpar skal ha 9 enkelbokser (3 ark). Du finner enkelboksene under "Kopiperm & trykkemateriell" i menyen til venstre.
En terning til hvert elevpar.
Fokus
Beskrivelse
Her kommer først en kort beskrivelse. For en utfyllende beskrivelse klikk i den gule boksen til høyre.
Elevene skal jobbe i par. Hvert elevpar lager mengdene 1-9 i enkelboksene med brikker, makaroni eller lignende.

Elevene skal nå jobbe sammen med å bygge mengdene på tallinja. Oppgaven bygges opp i vanskegrad og kompleksitet. Etter hvert skal elevene lage egne subtraksjonstykker.
 Rik oppgave: Subtraksjon med enkelbokser
Rik oppgave: Subtraksjon med enkelbokser


Introduksjon av oppgaven:
I denne oppgaven skal elevene deles i par og deretter jobbe med enkelbokser og brikker.
Enkelboksene finner du under "Kopiperm & trykkemateriell" i menyen til venstre.
Som brikker kan du bruke tellebrikker, noomer, makaroni, steiner, skjell eller hva som helst annet. Det eneste som er viktig å huske på er at brikkene ikke må være større enn rutene i enkelboksene. )
Hvert elevpar får 45 brikker og 9 enkelbokser (3 ark) hver.
Parene skal jobbe med å bygge mengdene på tallinja fra 1-9, og etter hvert med å lage egne subtraksjonstykker.
Lav inngangsterskel:
Del ut 45 brikker og 9 enkelbokser (3 ark) til hvert elevpar.
Elevene skal legge arkene på pulten og bygge mengder fra 1 til 9 som vist på bildet:

Neste nivå:
Del ut en trening til hvert elevpar.
Elevene skal kaste terning etter tur. Målet er å fjerne alle brikkene fra de ni ulike tallmengdene/enkelboksene. Den som klarer å fjerne siste brikken, har vunnet.
Et eksempel: Elev 1 kaster 5. Eleven kan da velge hvilken mengde den vil fjerne fem brikker fra. Si at eleven velger å fjerne hele 5-er mengden (enkelboksen med 5 i). Når eleven har gjort det, må han si: 5 - 5 = 0. Så er det elev 2 sin tur. Elev 2 kaster 3. Elev 2 velger å fjerne 3 fra 9-er mengden, og må si regnestykket: 9 - 3 = 6.
På den måten fortsetter aktiviteten til en av de to elevene har vunnet.
Hvis en elev kaster og treningen viser større sum enn noen av mengdene, så går turen videre til neste elev (man kan aldri ta bort brikker fra mer enn én mengde om gangen, og man må alltid "bruke opp hele terningen").
Åpen utgang:
La elevene som er klare for det diskutere strategi. Hva er lurt? Er det lurt å ta bort de små mengdene først, hvis en kan? Eller er det lurt å begynne å bryte ned de største mengdene?
La gjerne elevene forklare strategiene til de andre elevene, og se om det blir noe forskjell i spillemåten etter det.