< Tilbake

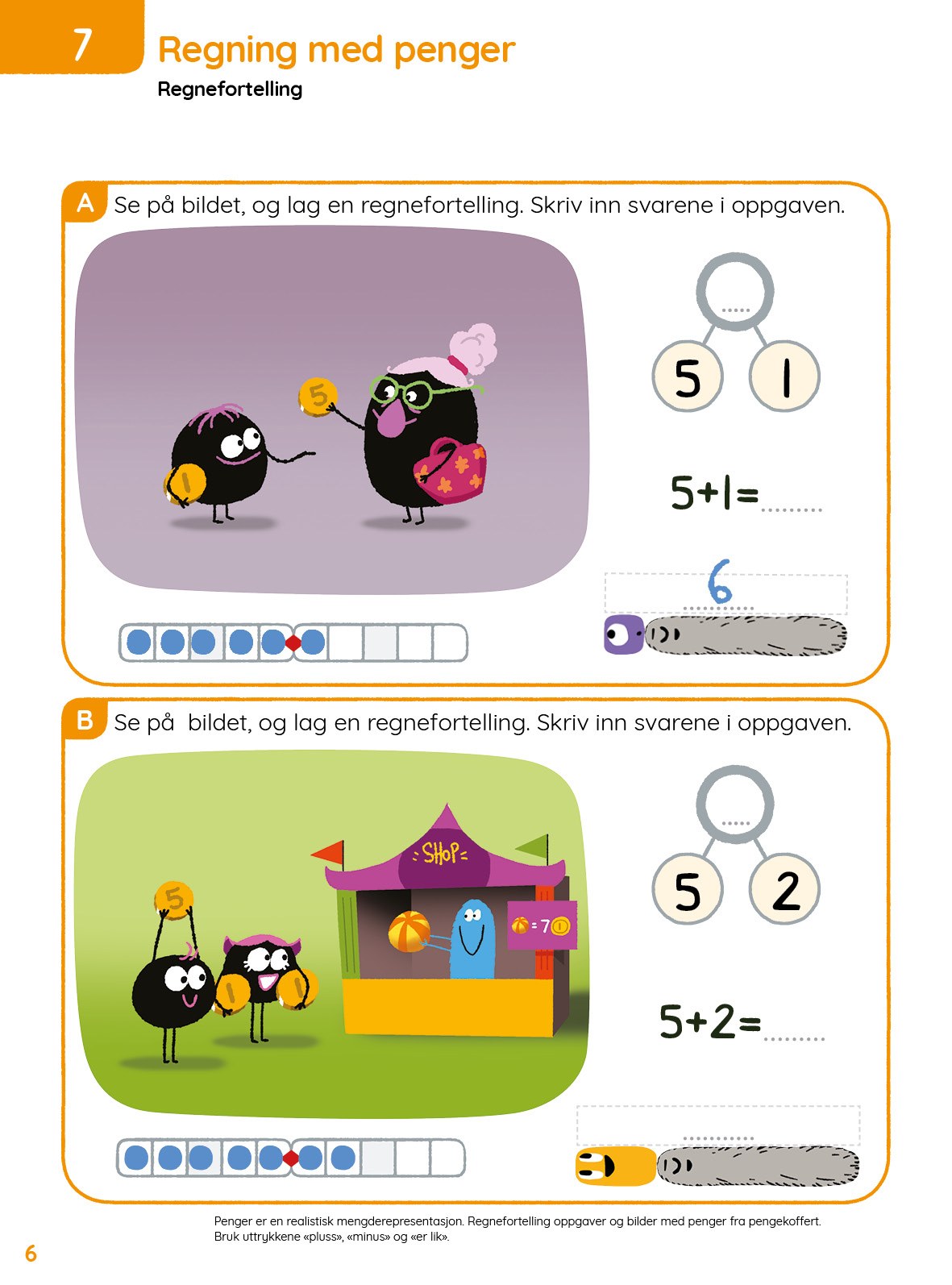
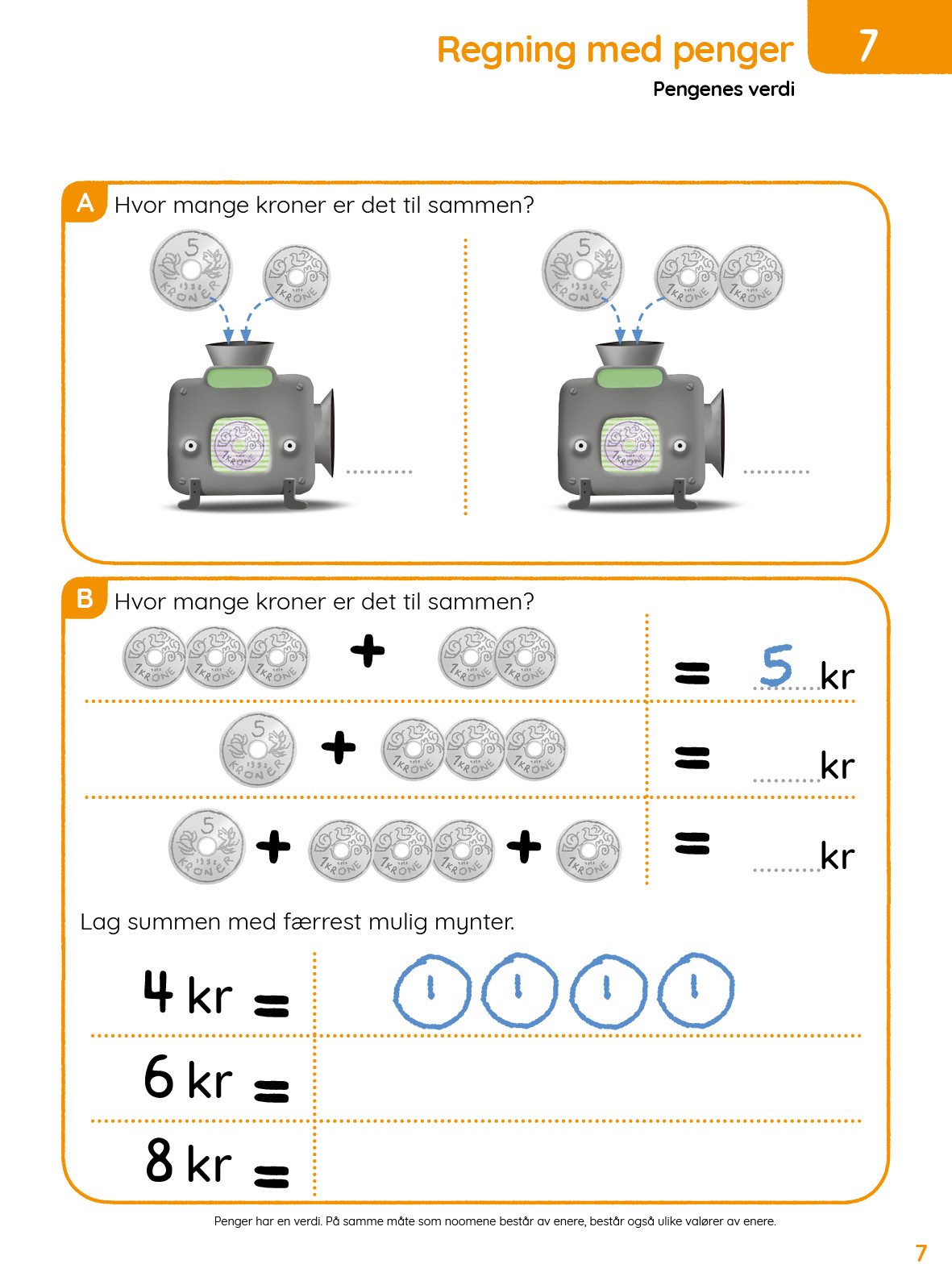
Tema 17: Penger 1 – 9 kr: En liten introduksjon og repetisjon av 5+_

Mål

Hovedmål:

Tolke og bruke mynter som modell i addisjon.
Forklare verdien av de forskjellige myntene vi bruker (1-kroning og 5-kroning).

Fokus

Denne uka er en repetisjon fra forrige halvår og en introduksjon av de første myntene.

Repetisjonen tar for seg:

tallene 6-9 som 5+x (5+1, 5+2, 5+3, 5+4).
tallvennemodellen, den usynlige noom og enkelboksen.
vanlige regnestykker med addisjon under 5 (3+2=, 2+2= osv).
vanlige regnestykker med «successor»-funksjonen opp til 10 (4+1=, 5+1=, 6+1= osv)

Introduksjon av mynter er en forsterking av tallene 6-9 som 5+x. Med 5-kroning og kronestykker skal elevene lage tallene 6-9 og tolke regnefortellinger med penger.

I økt 1 jobber elevene med 5+1 og 5+2. I Mattestreker skal elevene lage regnefortellinger med penger, fylle inn enkelboks, tallvennemodell og usynlig noom. I tillegg kommer noen vanlige regnestykker.

I økt 2 jobber elevene med 5+3, på samme måte som i økt 1.

I økt 3 jobber elevene med 5+4, på samme måte som i økt 1 og 2. I tillegg er det en logisk nøtt i Mattestreker. Denne oppgaven kan det være fint å jobbe med først parvis og deretter i plenum.

Den rike oppgaven i økt 4 handler også om mynter og pengesummer. Elevene skal jobbe i par, og hvert par skal ha mynter i en papirpose eller boks foran seg. Elevene trekker to og to mynter og regner ut pengesummene. Videre skal de finne ut hvor mange kombinasjoner som er mulige.

Hjemmelekse

Vårt forslag:

Elevene får mynter av foreldrene til å handle noe de trenger.
Mattesnakk side 50-51 (Duo slår av lyset).

Alternativt:

Sende hjem nettbrettet for å gjøre ferdig det som ikke ble ferdig forrige halvår.

Økt:

Ukas Øvingslab’er:

Vekslingsautomat: flere mynter

Tallrepresentasjoner

Tema 17: Penger 1 – 9 kr: En liten introduksjon og repetisjon av 5+_

Økt 1: Introduksjon til penger: 5+1 og 5+2

Mål

Elevene skal kunne:

Tolke enkel regnefortelling med addisjon av mynter, med støtte i bilde, modell og ligning.

Mattesnakk: (Repetisjon) Tallene 5-7

Vekslingsautomat: flere mynter: Med mynter 1, 5, 10 og 20

Tallrepresentasjoner: Med tall, noomer, penger, enkelboks og usynlig noom.

Mattestreker del 2: Introduksjon til penger: 5+1 og 5+2

Bilder til smartboard: Bilde

Likninger: Pengesummer 5+x

Tallvenner: 5+x

To og to: Noomer, tall, finger og terninger - opp til 10

Tallskriving: 3 til 9

Gardin: Likninger med enkelbokser eller fingre: Med enkelboks 5+x

Tallfakta: 5+x

Tallskriving: 3 til 9

To og to: Noomer, tall, finger og terninger - opp til 10

Tallvenner: x+1 og 5+x

Gardin: Tell penger.: Til 9

Sammenlikning: Fra 6 til 10

Tallmønstre: Tallrekker: opp til 10

< Tilbake

Mattesnakk: (Repetisjon) Tallene 5-7

< Tilbake

Vekslingsautomat: flere mynter: Med mynter 1, 5, 10 og 20

< Tilbake

Tallrepresentasjoner: Med tall, noomer, penger, enkelboks og usynlig noom.

< Tilbake

Mattestreker del 2: Introduksjon til penger: 5+1 og 5+2

< Tilbake

Bilder til smartboard: Bilde

< Tilbake

Likninger: Pengesummer 5+x

< Tilbake

Tallvenner: 5+x

< Tilbake

To og to: Noomer, tall, finger og terninger - opp til 10

< Tilbake

Tallskriving: 3 til 9

< Tilbake

Gardin: Likninger med enkelbokser eller fingre: Med enkelboks 5+x

< Tilbake

Tallfakta: 5+x

< Tilbake

Tallskriving: 3 til 9

< Tilbake

To og to: Noomer, tall, finger og terninger - opp til 10

< Tilbake

Tallvenner: x+1 og 5+x

< Tilbake

Gardin: Tell penger.: Til 9

< Tilbake

Sammenlikning: Fra 6 til 10

< Tilbake

Tallmønstre: Tallrekker: opp til 10

Tema 17: Penger 1 – 9 kr: En liten introduksjon og repetisjon av 5+_

Økt 2: Introduksjon til penger: 5+3

Mål

Elevene skal kunne:

Forklare verdien av de forskjellige myntene vi bruker (1-kroning og 5-kroning).

Mattesnakk: (Repetisjon) Tallet 8

Vekslingsautomat: flere mynter: Med mynter 1, 5, 10 og 20

Tallvenner: Med noomer og mynter

Mattestreker del 2: Introduksjon til penger: 5+3

Bilder til smartboard: Bilde

Likninger: Pengesummer 5+x

Tallvenner: x+1 og 5+x

Gardin: Likninger med enkelbokser eller fingre: Med enkelboks 5+x

Tallskriving: 3 til 9

Sammenlikning: Fra 0 til 10

Gardin: Tall med lyd.: Tall opp til 10

Tallvenner: x+1 og 5+x

Gardin: Likninger med enkelbokser eller fingre: Med enkelboks 5+x

Likninger: Pengesummer 5+x

Gardin: Tell penger.: Til 9

Tallmønstre: Tallrekker opp til 10

Tallninja: Tallninjen til 10

< Tilbake

Mattesnakk: (Repetisjon) Tallet 8

< Tilbake

Vekslingsautomat: flere mynter: Med mynter 1, 5, 10 og 20

< Tilbake

Tallvenner: Med noomer og mynter

< Tilbake

Mattestreker del 2: Introduksjon til penger: 5+3

< Tilbake

Bilder til smartboard: Bilde

< Tilbake

Likninger: Pengesummer 5+x

< Tilbake

Tallvenner: x+1 og 5+x

< Tilbake

Gardin: Likninger med enkelbokser eller fingre: Med enkelboks 5+x

< Tilbake

Tallskriving: 3 til 9

< Tilbake

Sammenlikning: Fra 0 til 10

< Tilbake

Gardin: Tall med lyd.: Tall opp til 10

< Tilbake

Tallvenner: x+1 og 5+x

< Tilbake

Gardin: Likninger med enkelbokser eller fingre: Med enkelboks 5+x

< Tilbake

Likninger: Pengesummer 5+x

< Tilbake

Gardin: Tell penger.: Til 9

< Tilbake

Tallmønstre: Tallrekker opp til 10

< Tilbake

Tallninja: Tallninjen til 10

Tema 17: Penger 1 – 9 kr: En liten introduksjon og repetisjon av 5+_

Økt 3: Introduksjon til penger: 5+4

Mål

Elevene skal kunne:

Forklare at tallet på prislappen av en vare viser varens verdi

Mattesnakk: Introduksjon til tallet 9

Mattesnakk: En tallgåte

Vekslingsautomat: flere mynter: Med mynter 1, 5, 10 og 20

Tallrepresentasjoner: Med tall, noomer, penger, enkelboks og usynlig noom.

Mattestreker del 2: Introduksjon til penger: 5+4

Bilder til smartboard: Bilde

Likninger: Pengesummer 5+x

Tallvenner: x+1 og 5+x

Tallskriving: 3 til 9

Gardin: Likninger med enkelbokser eller fingre: Med fingre og enkelbokser 5+x

Tallfakta: x+1 og 5+x

Likninger: Pengesummer 5+x

Tallvenner: x+1 og 5+x

Fingre: Hvor mange fingre? Under 10

< Tilbake

Mattesnakk: Introduksjon til tallet 9

< Tilbake

Mattesnakk: En tallgåte

< Tilbake

Vekslingsautomat: flere mynter: Med mynter 1, 5, 10 og 20

< Tilbake

Tallrepresentasjoner: Med tall, noomer, penger, enkelboks og usynlig noom.

< Tilbake

Mattestreker del 2: Introduksjon til penger: 5+4

< Tilbake

Bilder til smartboard: Bilde

< Tilbake

Likninger: Pengesummer 5+x

< Tilbake

Tallvenner: x+1 og 5+x

< Tilbake

Tallskriving: 3 til 9

< Tilbake

Gardin: Likninger med enkelbokser eller fingre: Med fingre og enkelbokser 5+x

< Tilbake

Tallfakta: x+1 og 5+x

< Tilbake

Likninger: Pengesummer 5+x

< Tilbake

Tallvenner: x+1 og 5+x

< Tilbake

Fingre: Hvor mange fingre? Under 10

Tema 17: Penger 1 – 9 kr: En liten introduksjon og repetisjon av 5+_

Økt 4: Rik oppgave: Mynter i posen

Mål

Elevene kan utforske ulike mynter og pengesummer knyttet til disse.

Ekstra utstyr

Penger/lekepenger/papirkopier av penger. Hvert par av elever trenger tre 1-kroninger, to 5-kroninger og en 10-kroning.
Papirpose, boks eller lignende som man ikke kan se gjennom. Hvert par av elever trenger en stk hver.
Skrivesaker og skrivebok/skrivebrett/blanke ark.

Beskrivelse

Her kommer først en kort beskrivelse. For en utfyllende beskrivelse klikk i den gule boksen til høyre.

I denne oppgavene skal elevene jobbe i par. Hvert elevpar har tre kronestykker og én 5-kroning foran seg i en papirpose eller boks.

Elevene skal nå trekke to mynter, og deretter regne ut pengesummen.

Oppgaven utvides til å gjelde andre mynter og ulike vrier på oppgavene.

Rik oppgave: Mynter i posen

< Tilbake

Rik oppgave: Mynter i posen

I denne oppgaven skal elevene deles i par og deretter jobbe med mynter. Elevene har tre kronestykker og én 5-kroning hver. Parene skal jobbe med kombinasjoner og pengesummer knyttet til disse myntene.

Introduksjon av oppgaven:

Del ut tre kronestykker, én 5-kroning og en papirpose eller boks som man ikke kan se gjennom til hver av elevparene.
Repeter verdien av myntene.
Hvilken pengesum får jeg dersom jeg trekker to kronestykker opp av posen? Still dette spørsmålet til elevene og la dem skrive ned fremgangsmåte/regnestykke og svaret i egen bok eller på eget skrivebrett.
Jobb med oppgaven i plenum:
- Snakk om fremgangsmåte (fysisk ved å vise med myntene på tavla og myntene elevene har foran seg).
- Regnestykke (1+1=2) og svaret (2 kr).
Gjenta de to foregående punktene med spørsmålet: Hvilken sum får jeg dersom jeg trekker to 1-kroninger og én 5-kroning ut av posen?
Gjenta dette med liknende spørsmål til elevene forstår hvordan de fysisk skal jobbe med myntene foran seg, lage/skrive regnestykker knyttet til myntene og finne pengesummer.

Lav inngangsterskel:

Del elevene i par.
Påse at hvert elevpar har tre kronestykker, én 5-kroning og en papirpose hver.
Én av elevene i hvert par starter ved å trekke to mynter opp av poasen. Hvilken pengesum ble det? Elevene skal snakke om dette i par, så skal begge elevene skrive ned det aktuelle regnestykket og komme med svar.
Deretter er det den andre eleven i paret som trekker to mynter, og prosessen ovenfor gjentas.
Hvor mange kombinasjoner og summer er det mulig å få med disse myntene? La elevene jobbe parvis med denne oppgaven.
Snakk sammen om oppgaven i plenum eller gruppevis før elevene begynner med neste nivå.

Neste nivå:

Elevene jobber fremdeles i par.
Elevparene får bytte det ene kronestykket de har mot én 5-kroning, slik at de nå har to kronestykker og to 5-kroninger i posen. Det er fremdeles kun to mynter som skal trekkes opp av posen.
Spør elevene om følgende: Er det fremdeles de samme pengesummene de kan få? Hvorfor/hvorfor ikke?
La elevparene nå utforske den nye situasjonen ved å jobbe som ovenfor (trekke to mynter, skrive ned regnestykket, trekke to nye mynter, skrive ned regnestykket).
Snakk sammen i plenum om resultatet. Hvorfor får de andre pengesummer? Hvilke pengesummer kan de få nå?

Åpen utgang:

Hvilke mynter må elevparene ha hvis de skal kunne trekke to mynter som gir summen 15 kroner? La dem få myntene de mener de trenger, slik at de kan sjekke om de har tenkt riktig eller evt hva de har tenkt som ikke er helt riktig.
Hvilke mynter må de ha dersom de skal kunne trekke summene 15 kroner, 11 kroner og 2 kroner ved å trekke to mynter?
La elevene få en 10-kroning, to 5-kroning og tre kronestykker.
- Kan de finne noen pengesummer det ikke er mulig å lage når de bare kan trekke to mynter?
- Hvor mange mynter må de trekke for å kunne lage pengesummen 16?
- Hvor mange mynter må de trekke for å kunne lage pengesummen 17?
- Hvor mange mynter må de trekke for å kunne lage pengesummen 12? Finnes det flere alternativer?
Hvis det er mer tid igjen, kan elevene nå lage oppgaver til hverandre, enten innad i paret eller mellom parene.