Tema 23: Tall og telling, tallmønstre og symmetri
Mål
Hovedmål:
Sette ord på sine tanker og erfaringer i møte med tallfølger og mønstre.
Benytte hensiktsmessige tellestrategier når man skal telle uoversiktlige mengder.
Fokus
Denne uka introduseres elevene for tellestrategier, tallmønster og symmetri.
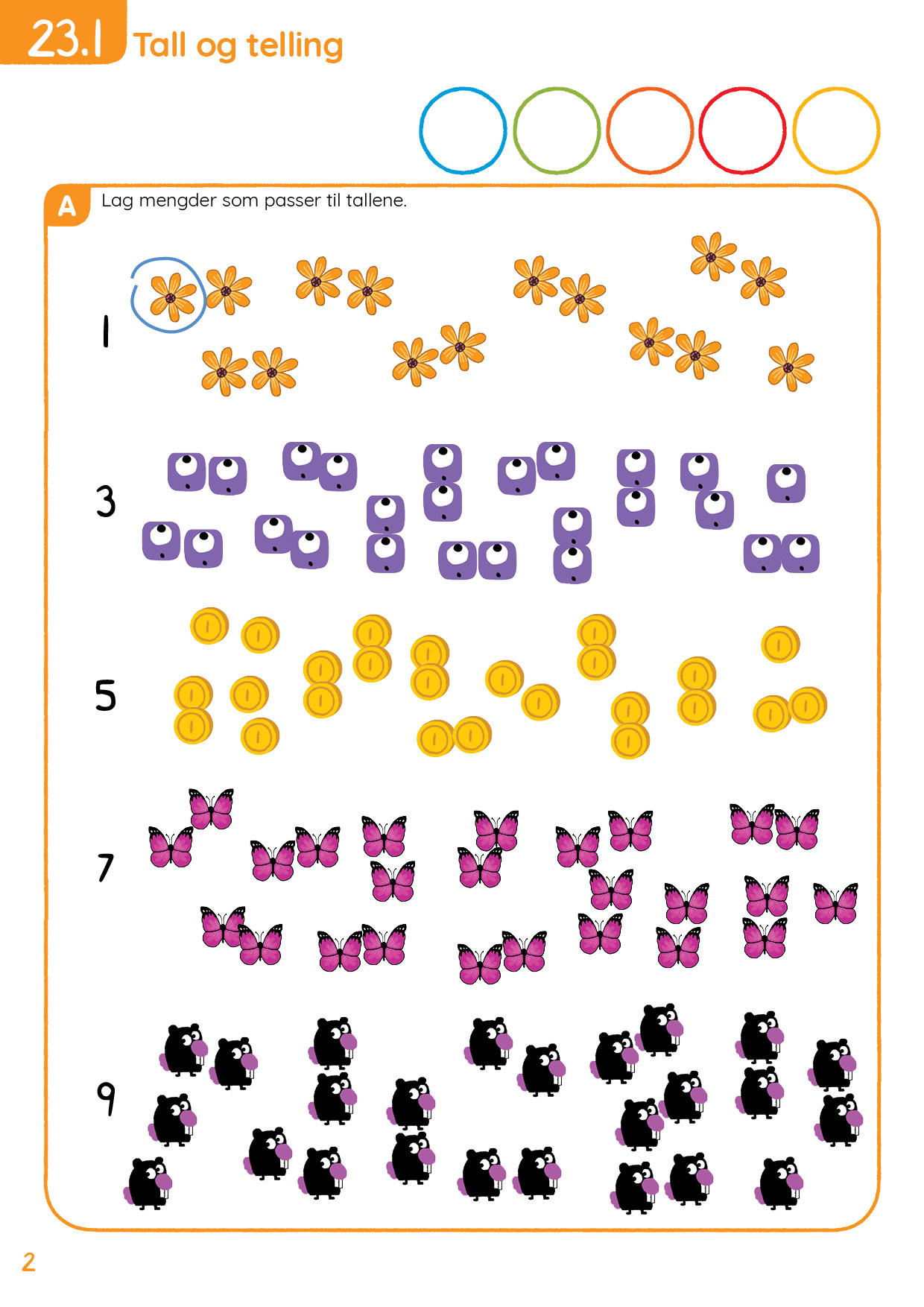
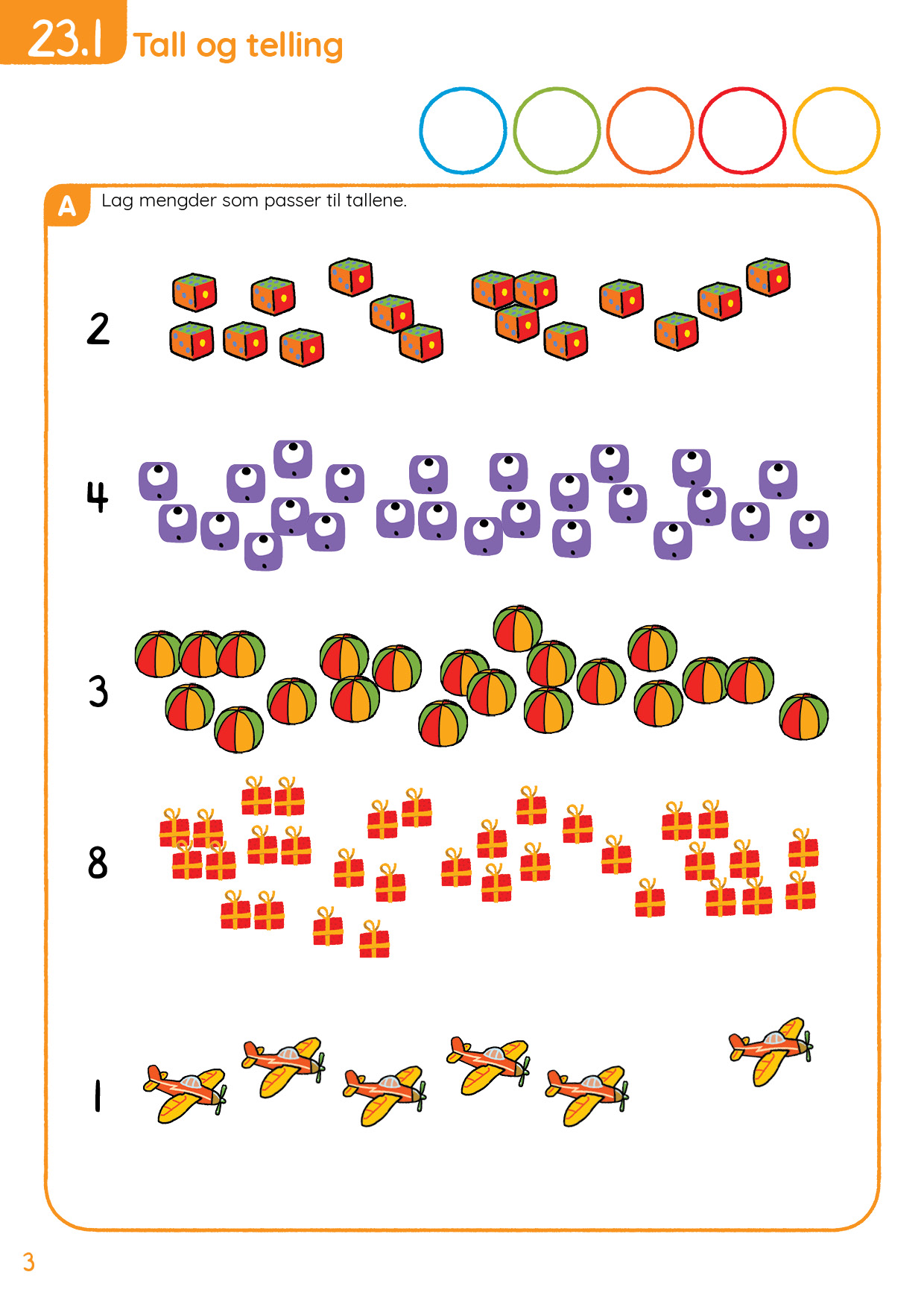
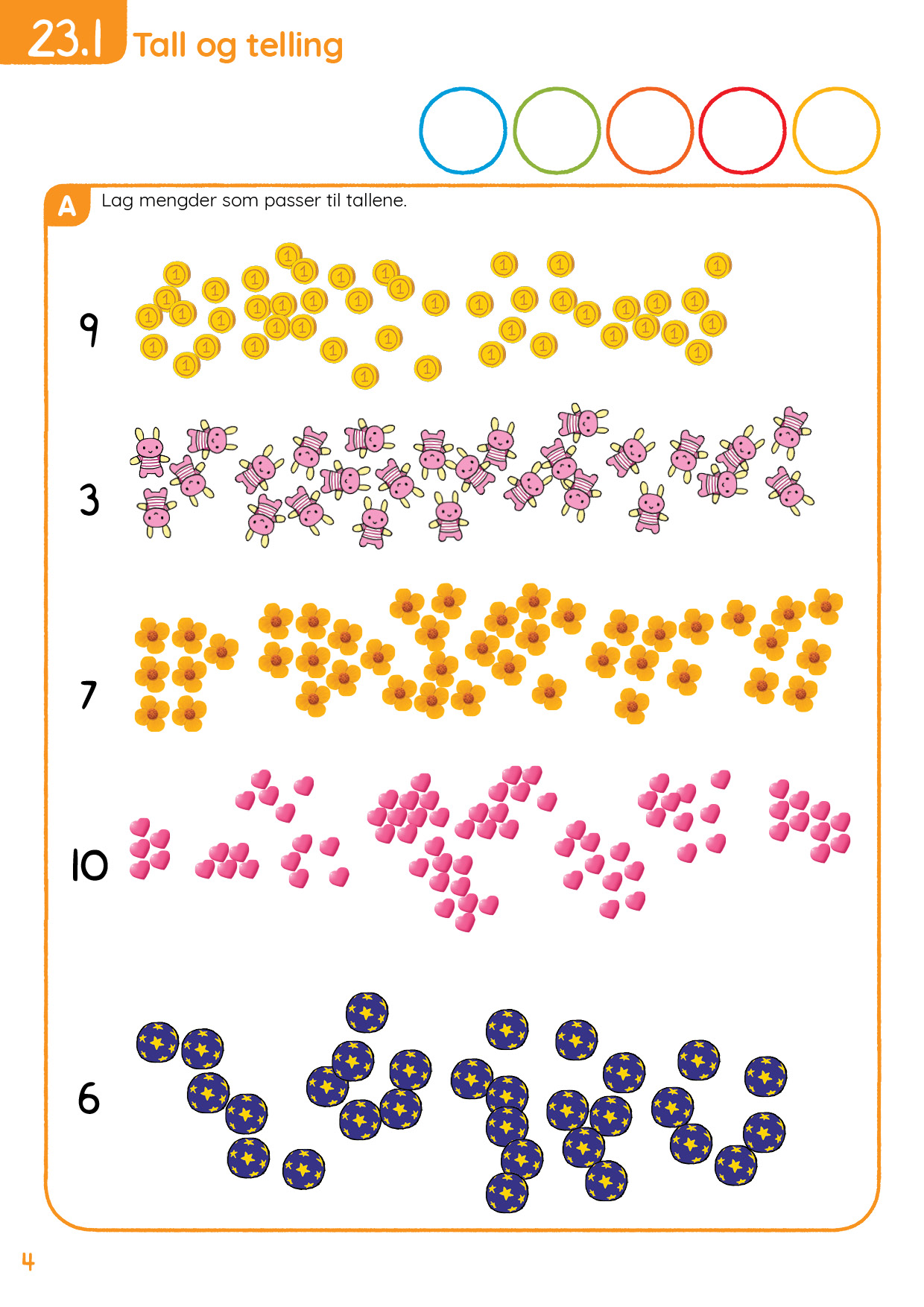
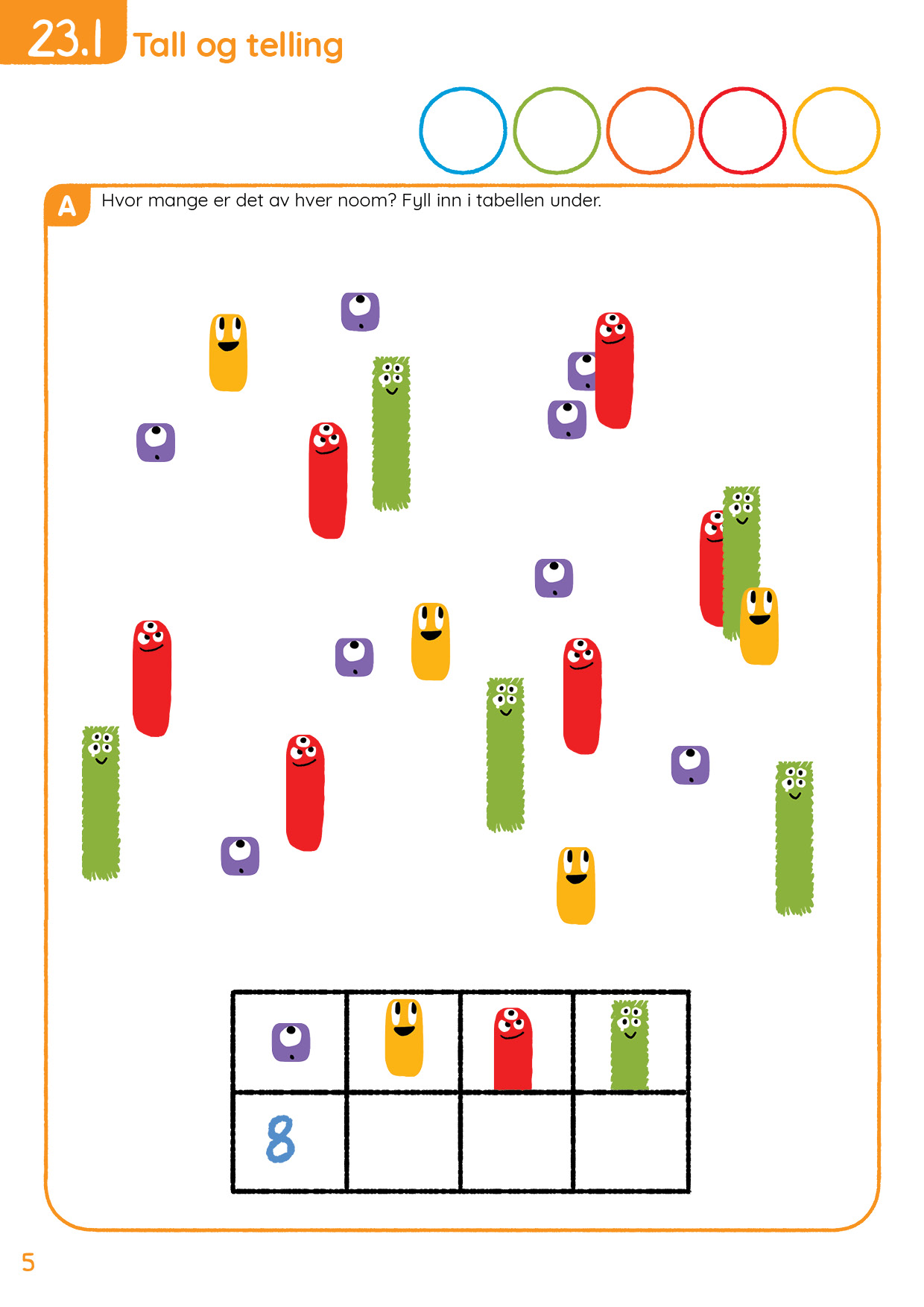
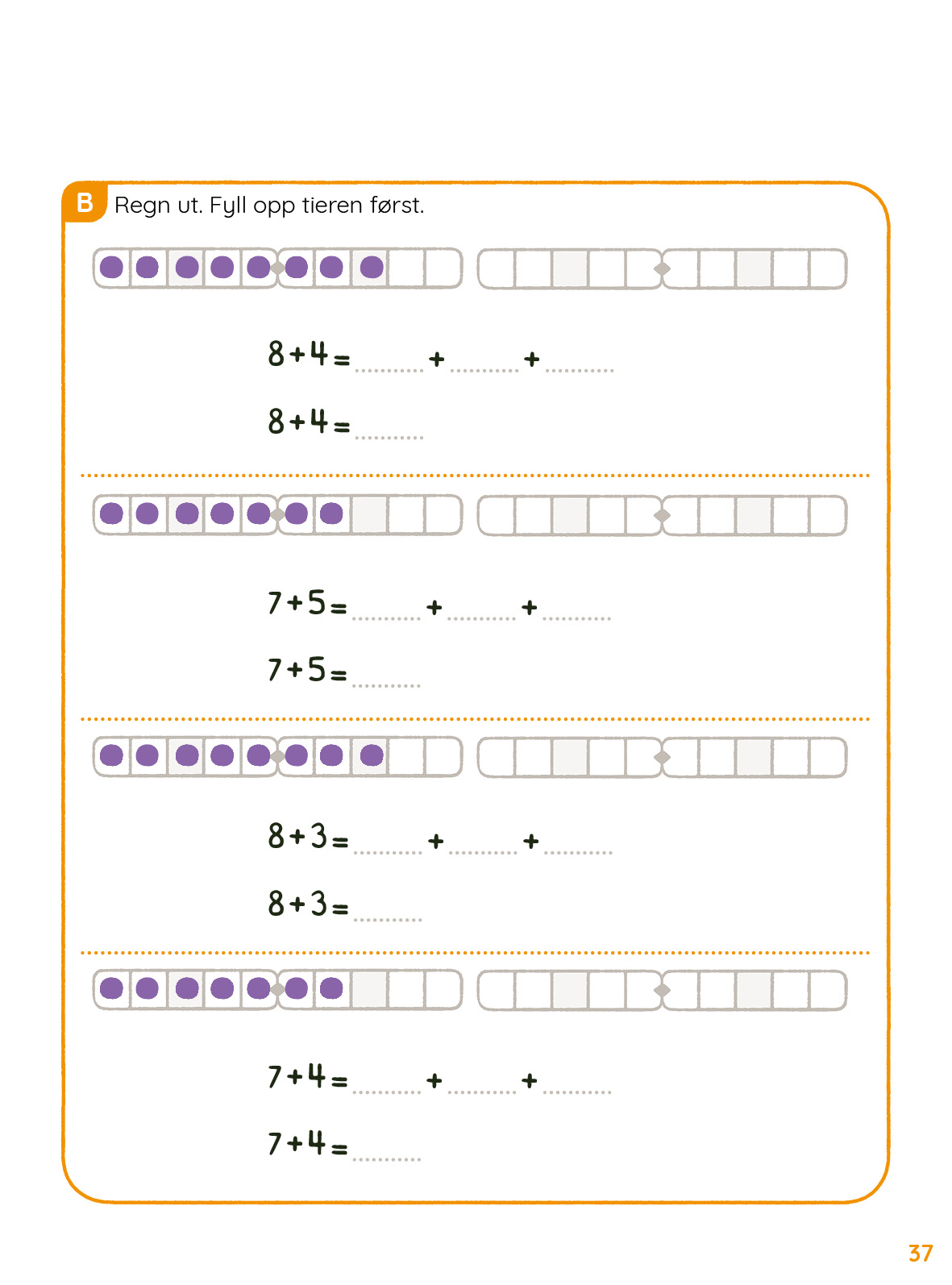
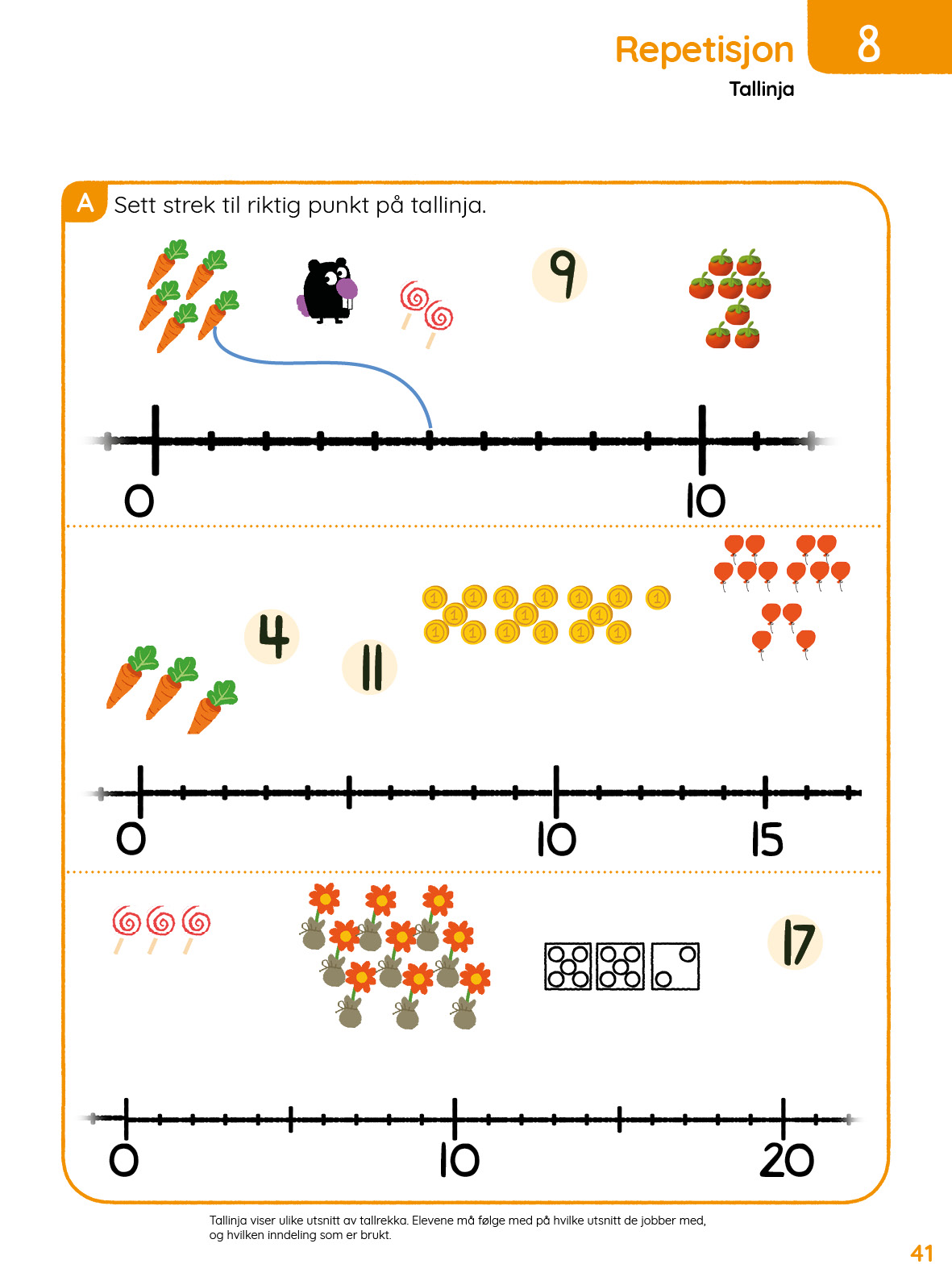
I økt 1 jobber elevene med tellestrategier. Elevene skal telle mengder som ikke er grupperte. Det er flere strategier for å telle riktig:
Gruppere mengden i 5-er grupper. Denne strategien passer bra når det kun er én type objekt som skal telles, og det er lett for elevene å sjekke om det de kom frem til var riktig.
Krysse av objektene som er telt. Denne strategien hjelper for å sjekke at man har telt alle objekter, men det er vanskelig for elevene å kontrollere svaret etterpå.
Tegne en linje som går gjennom de objektene som skal telles. Denne strategien passer bra når man har flere ulike objekter som skal telles, der objektene er blandet. Elevene kan kontrollere at de har telt alle objektene ved å sjekke at alle objektene har en linje gjennom seg. Det er også enkelt å kontrollere antallene ved å følge linjen fra start til slutt og telle alle objektene på linja en gang til.
Vi anbefaler sistnevnte tellestrategi for side 35 og 37 i Mattestreker denne økta. Det er fint å starte økta med først å la elevene selv komme med forslag til ulike måter å telle på. Hvordan kan man være sikker på å ha telt alle tingene? Hvordan kan man være sikker på at antallet stemmer? Kanskje har elevene noen bedre forslag en det vi har der?
På økt-siden ligger det 6 sider ekstra som man kan bruke på smartboarden. Disse sidene ligner på de sidene elevene møter i Mattestreker. Bruk gjerne disse sidene når dere utforsker ulike tellestrategier sammen. La alle elevene få oppleve og forstå hvordan de kan bruke lure tellestrategiene før de jobber alene i Mattestreker.
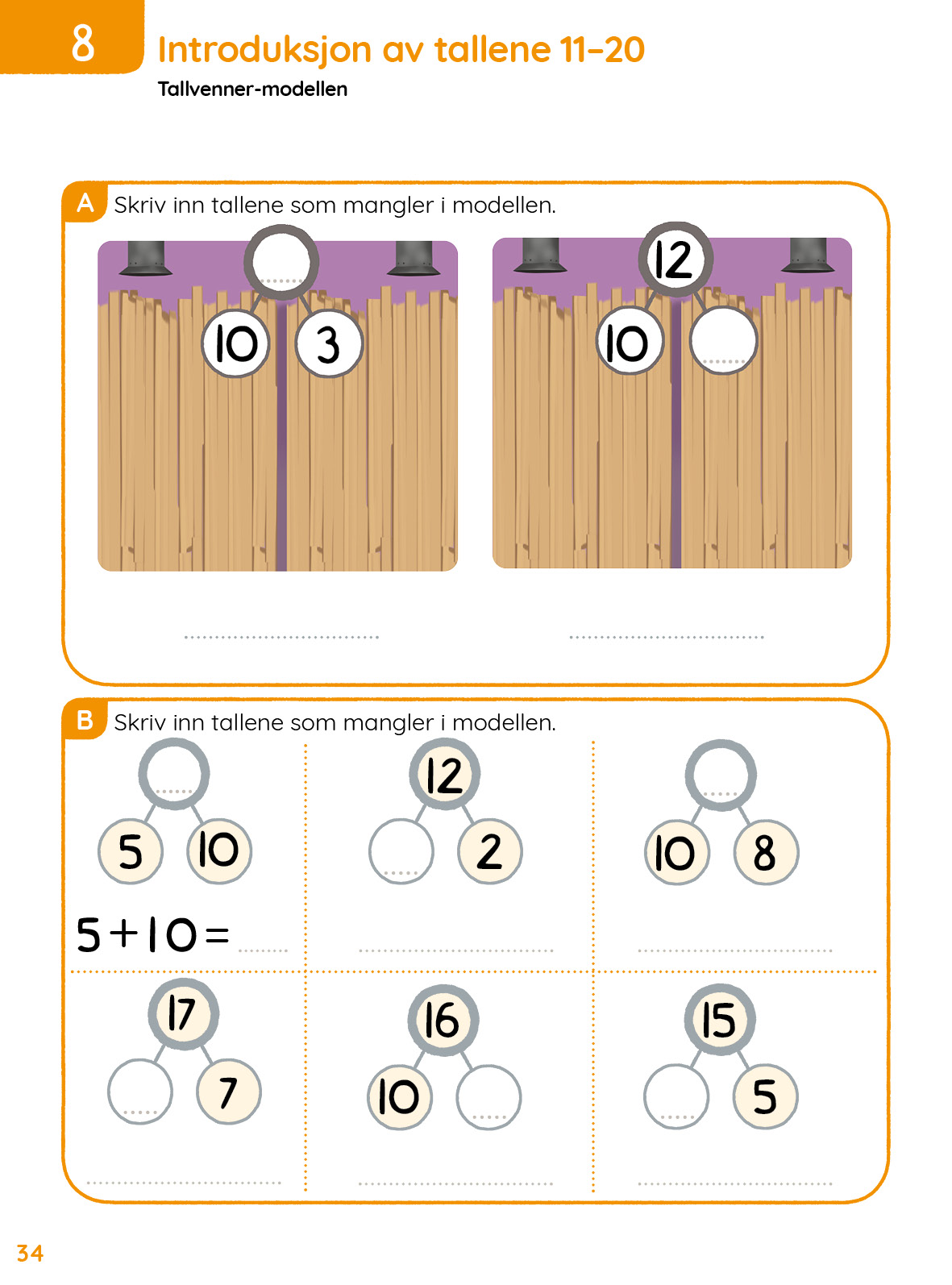
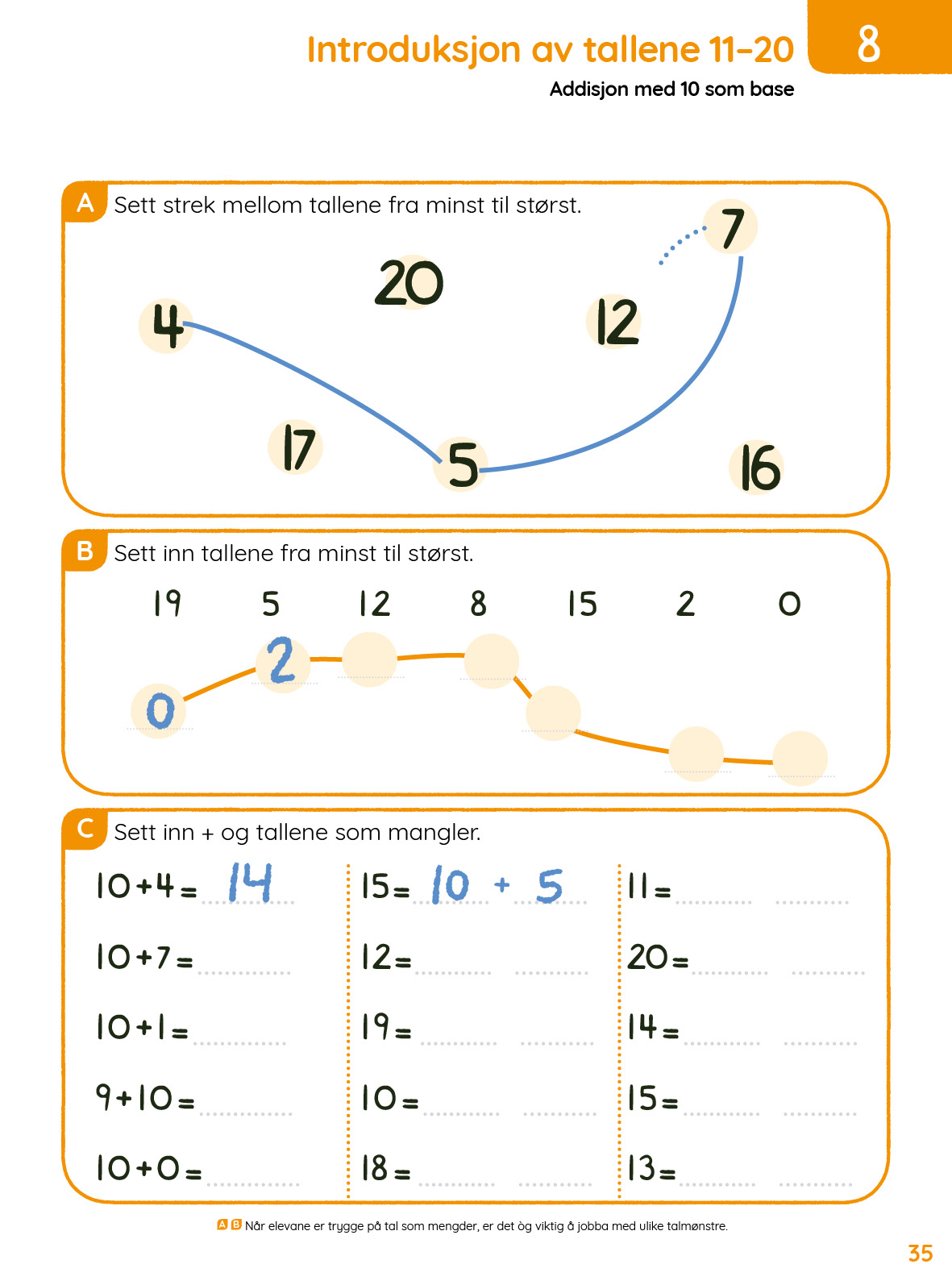
I Mattestreker er det også en oppgave om nabotall. Nabotall er fint å ta for seg gjennom hele året. Man kan snakke om hvilke tall som ligger før og etter dagens dato, og man kan gjøre det mer avansert med å spørre om hvilke to tall som ligger før eller etter dagens dato. Man kan også bruke nummeret på måneden vi er i, bursdagsdatoer, alder på ulike familiemedlemmer med mer. For de mest avanserte elevene kan man gjøre samme øvelse med årstallet vi har i dag, eller årstallet de er født.
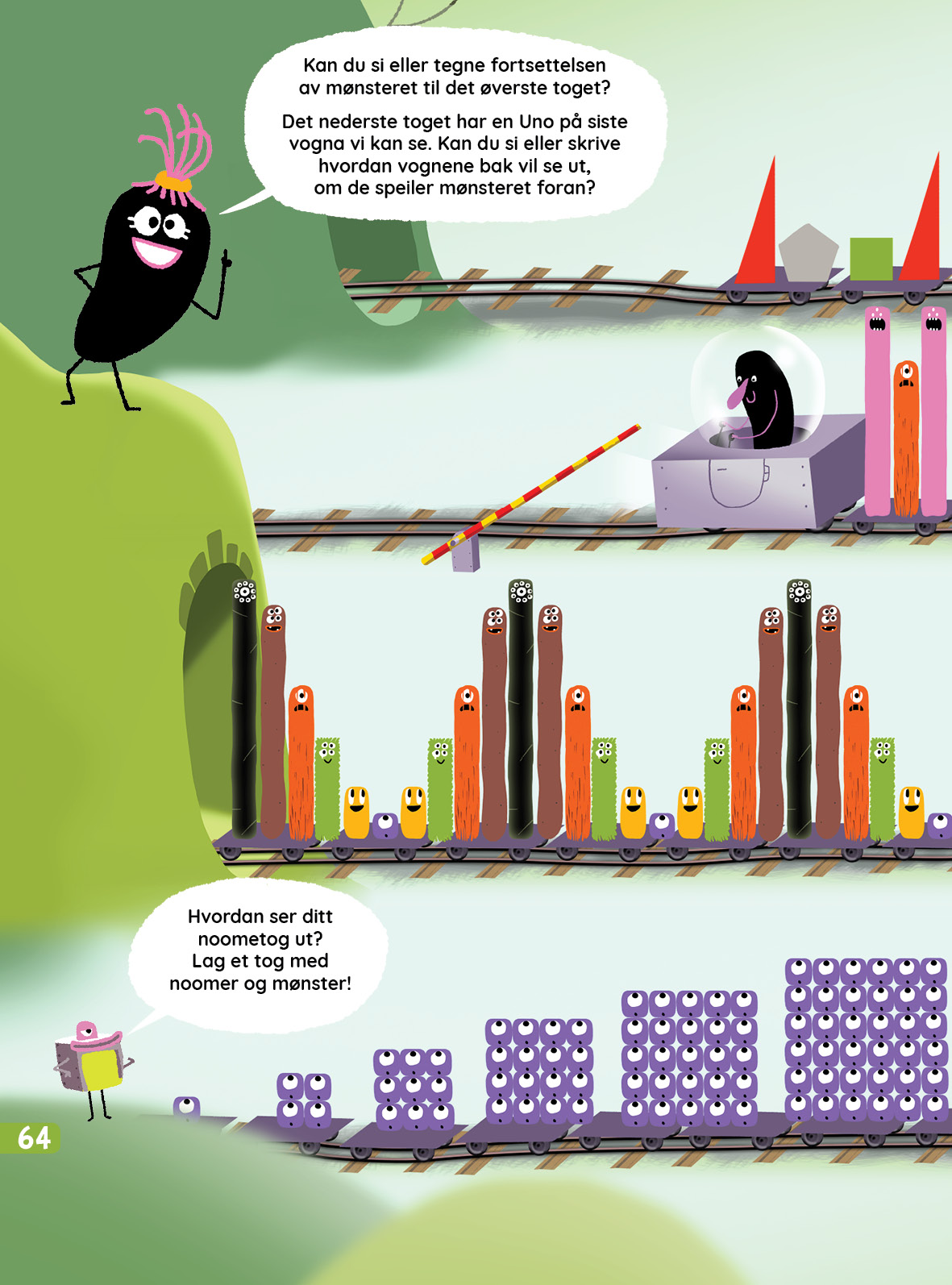
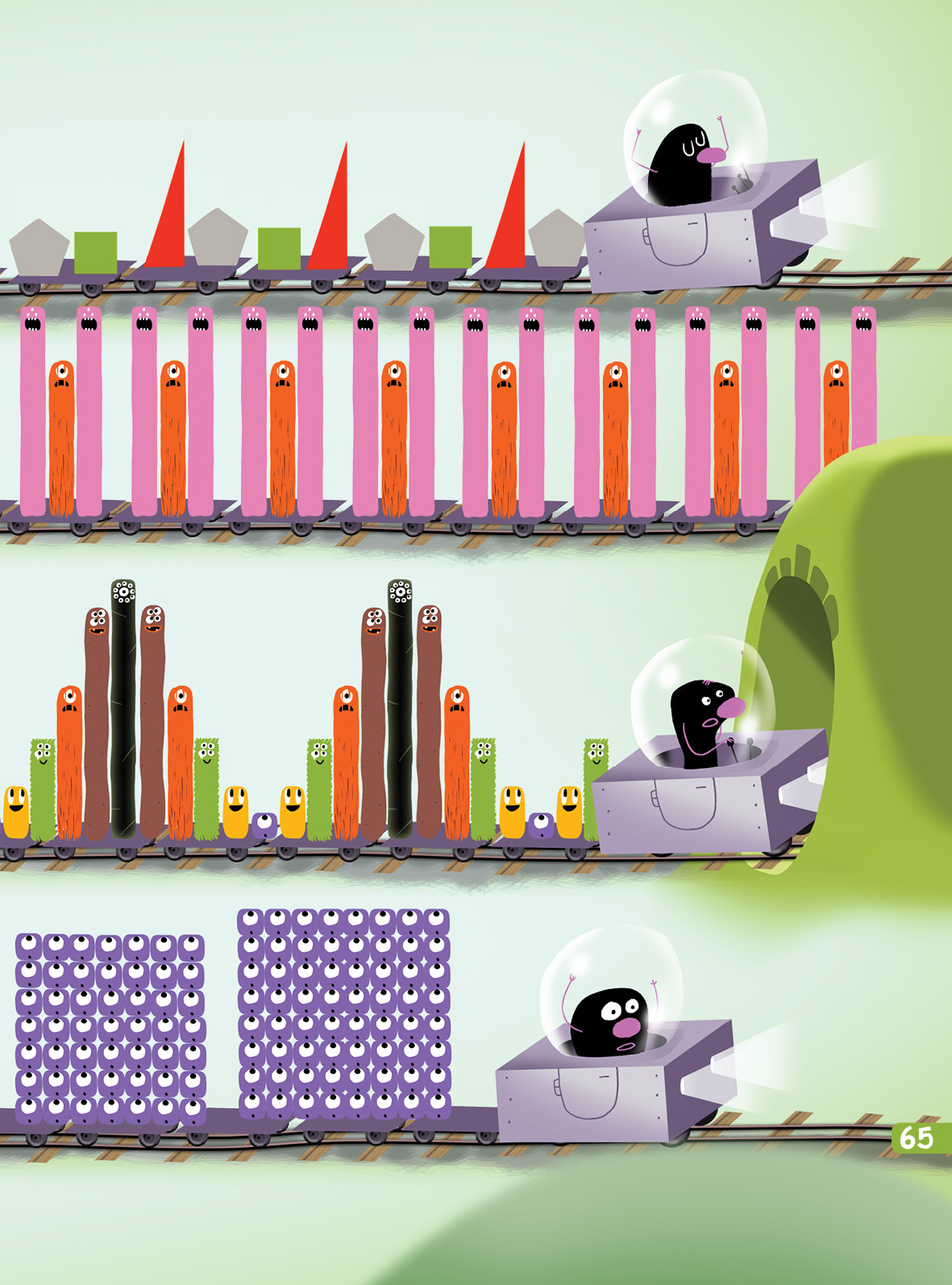
I økt 2 jobber elevene men tallmønster. I tillegg til Mattesnakk, kan dere også lage mønster med de fysiske noomstavene. Husk da å også skrive tallsymbolene, slik at elevene øver seg å kjenne igjen tallmønster uten konkreter. Det er også fint å bruke øvingslabben Tallrepresentasjoner til å lage tallmønster. Bruk noomene, terninger, mynter, fingre eller enkelboksen til å lage mønster, og bruk tallene slik at elevene også ser mønsteret med tallsymboler.
I Økt 3 jobber elevene med symmetri og symmetrilinjer. Det er en egen øvingslab knyttet til dette som heter ”Symmetri og symmetrilinje”. Denne øvingslabben er veldig gøy å leke med, så for å få best resultat er det lurt å la elevene selv få utforske denne øvingslabben på nettbrettet sitt før dere utforsker den i plenum. Husk å bruke begrepet ”symmetri” og begrepet ”symmetrilinje”. Etter at elevene er ferdige med Mattestreker er det fint å la elevene få utforske og leke litt mer med øvingslabben. På denne økes læringsutbyttet.
Den rike oppgaven i økt 4 handler også om nabotall og tallmønster.
Lurt å Vite
Hjemmelekse
 Skriv Ut
Skriv Ut
Økt 1: Tall og telling
Mål
Elevene skal kunne:
Bruke hensiktsmessige tellestrategier når de teller uoversiktlige mengder.
Kjenne igjen nabotall og kunne fylle inn nabotall som mangler.
Ekstra utstyr
Fokus
Beskrivelse
Økt 2: Tallmønstre
Mål
Elevene skal kunne:
- Kjenne igjen tallmønster og kunne fylle inn tall som mangler i et tallmønster.
Ekstra utstyr
Fokus
HUSK: Et tallmønster har uendelig mange måter å fortsette på. Så det er ikke sikkert eleven tenker «feil» selv om svaret er annerledes enn det du hadde tenkt. Spør alltid eleven om hvordan han/hun tenker.
Beskrivelse
Økt 3: Symmetri
Økt 4: Rik oppgave: Tallmønster
Mål
Elevene forstår og kan fylle ut tallmønstre.
Ekstra utstyr
Tallkort fra 0 til 9 (ett sett til hvert elevpar). Du finner tallkort under ”kopiperm og trykkemateriell” i lærerveiledningen.
Tallkort 10 – 19 til de eleveparene som trenger større utfordringer. Se tips under her til hvordan man lager disse tallkortene.
Tre svarte papirlapper til hvert elevpar. En papirlapp må ha samme størrelse som et tallkort.
Fokus
TIPS!
Det er viktig at elevene forstår at et tosifret tall består av både tiere og enere. Hvis vi tar bort 2-tallet fra 12, så står det ikke 1 der, men det står 10. Ved å bruke tallkortene våre lærere elevene dette automatisk. Når vi lager 12, så bruker vi tallkortene 10 og 2. 2-kortet settes over 0 på denne måten:
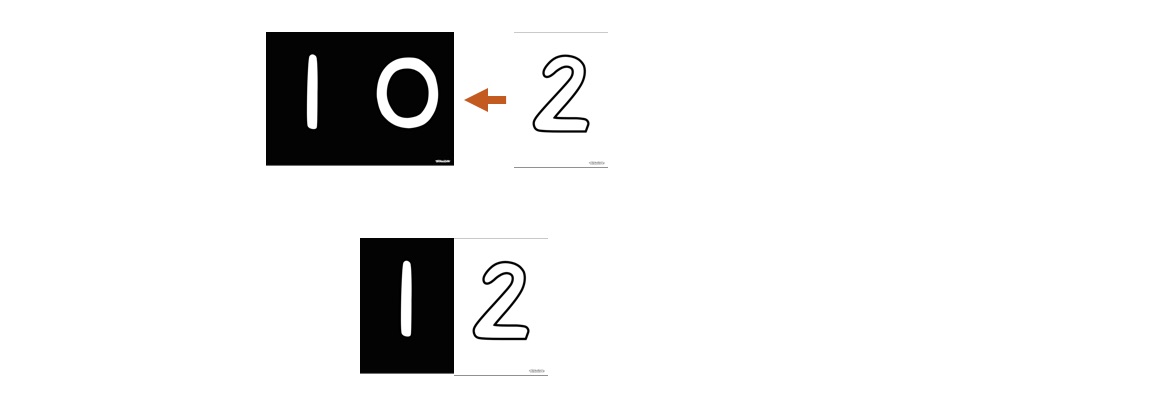
For at et elevpar skal lage tallene 10-19, så trenger de derfor følgende:
10 stk av tallkortet 10.
Tallkortene 1-9.
Vær oppmerksom på at dette er hva ett elevpar trenger. Hvis det er flere elevpar så trengs alle disse kortene til hvert elevpar.
Beskrivelse
Her kommer først en kort beskrivelse. For en utfyllende beskrivelse klikk i den gule boksen til høyre.
Elevene skal jobbe i par. Ved oppstart legger hvert elevpar tallkortene i rekkefølge fra 0 til 9.

Elevene skal nå jobbe sammen og øve på å kjenne igjen nabotallene. Oppgaven bygges opp i vanskegrad og kompleksitet. Etter hvert skal elevene øve seg på å lage partalls- og oddetalls-mønstre, eller andre tallmønstre.
 Rik oppgave: Tallmønster
Rik oppgave: Tallmønster
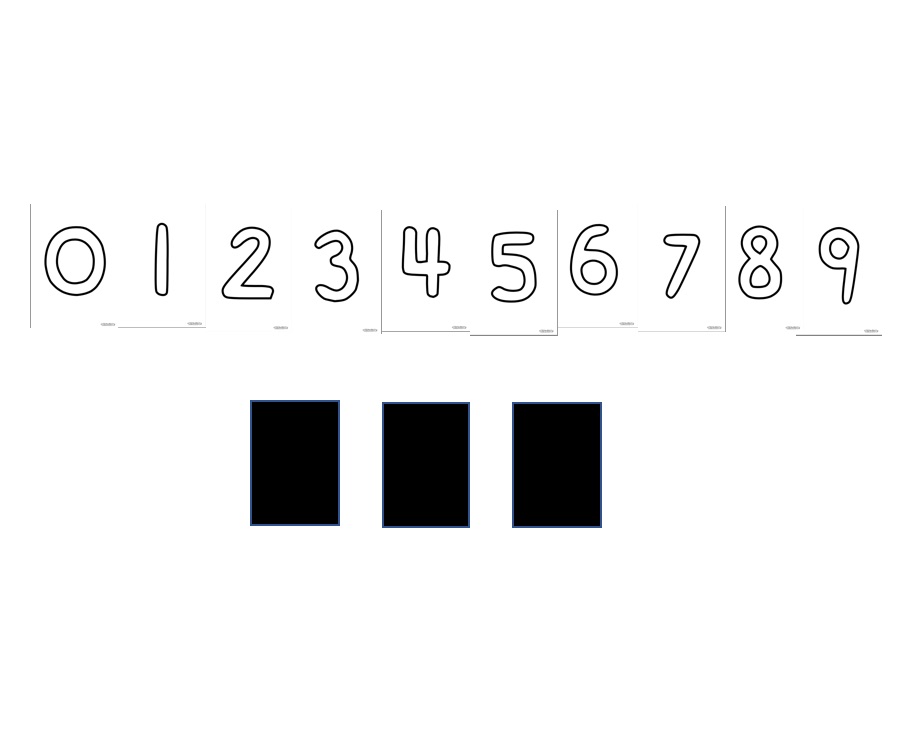
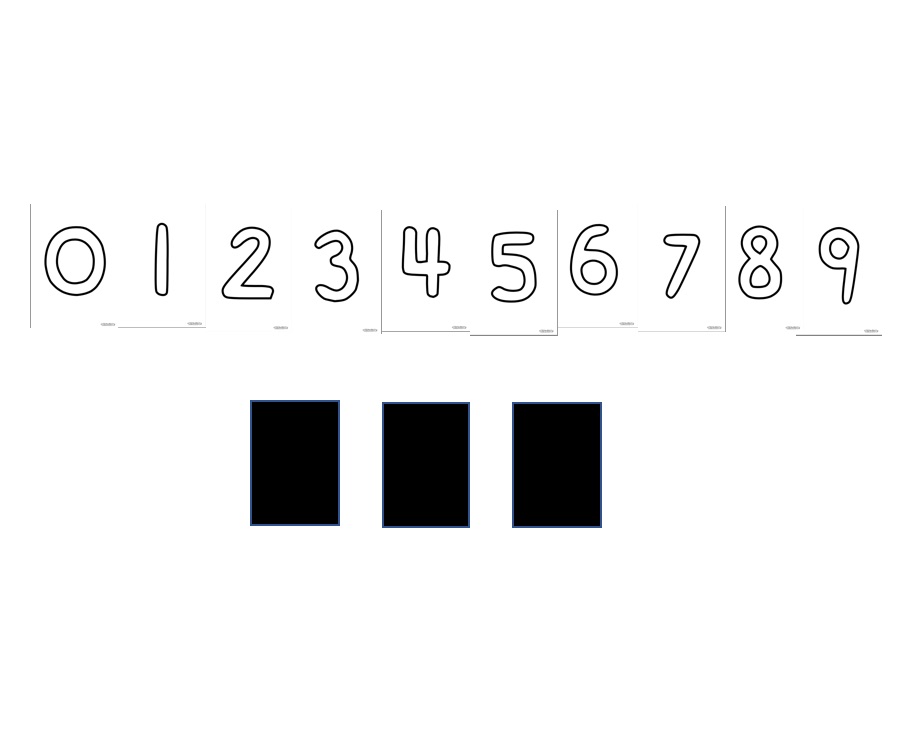
Introduksjon av oppgaven:
I denne oppgaven skal elevene deles i par og deretter jobbe med tallmønster. Hvert elevpar får tallkort 0-9 og tre svarte lapper hver. Elevene skal jobbe med å kjenne igjen nabotall og tallmønster.
Lav inngangsterskel:
Skriv tallene 0 til 9 i stigende rekkefølge på tavla. Be elevene holde hendene for øynene legge hodet på pulten.
Visk bort to av tallene fra tavla.
Elevene skal nå finne ut hvilke tall som er visket bort.
Elevene fortsetter med samme aktivitet i par. Eneste forskjellen nå er at de ikke visker bort tall, men de legger de svarte lappene over tallkort. Dette gjøres slik:
Elev 1 lukker øynene, elev 2 skjuler tre tall med lappene.
Elev 1 åpner øynene og forteller hvilke tall elev 2 har skjult.
Elev 2 tar så bort lappene for å sjekke om det stemte.
Deretter går det på omgang å skjule tallene.
TIPS: Hvis oppgaven er for vanskelig for noen av parene kan man starte med bare en eller to svarte lapper, og deretter øke til tre.
Neste nivå:
De elevparene som mestrer den første oppgaven, kan nå få i oppgave å lage tallmønster med bare partallene eller bare oddetallene i tallområdet 0-9. De lager seg et mønster med
* oddetallene (1 – 3 – 5 – 7 – 9 ) og et med * partallene (0-2 – 4 – 6 - 8).Etter at de har lagt tallkortene i disse to mønstrene, fortsetter de aktiviteten over. Elev 1 skjuler tall med brikker (kan være lurt å starte med en brikke og øke til tre etter hvert), mens elev to lukker øynene.
Det er også fint å lage tallmønsteret andre veien: 9-7-5-3-1 og 8-6-4-2-0.
Åpen utgang:
De elevene som trenger ekstra utfordringer kan nå også få tallkortene 10-19. På øktsiden (23.4) er det beskrevet hvordan man lager disse tallkortene.
Forklar elevparene hvordan tallene lages med tallkortene, og la dem først legge 0-19 i stigende rekkefølge. Elev 1 lukker så øynene mens elev 2 legger på de svarte lappene (OBS: For tallene 10-19 trengs enten større lapper eller to lapper for hvert talls om skal skjules).
Etterhvert kan de prøve seg på andre tallmønster. Be dem utforske hva slags tallmønster de kan lage med lappene, og be dem beskrive mønstrene.
For å øke vanskelighetsgraden ytterligere, så kan elev 2 lage et tallmønster mens elev 1 lukker øynene. Elev 1 fortsetter å lukke øynene mens elev 2 tar på svarte lapper. Nå skal elev 1 både prøve å finne ut hva slags mønster som er laget, beskrive det og også finne ut hvilke tall som mangler.