Tema 7: Uformell addisjon (uten '+' -tegnet)
Mål
Elevene skal kunne:
- Visualisere mengder under 5 på forskjellige måter, med støtte i modell (tall, noomer, tallvenner).
- Lage enkel regnefortelling med addisjon, med støtte i bilde og modell (tallvenner).
- Tolke enkel regnefortelling med addisjon, med støtte i bilde.
Fokus
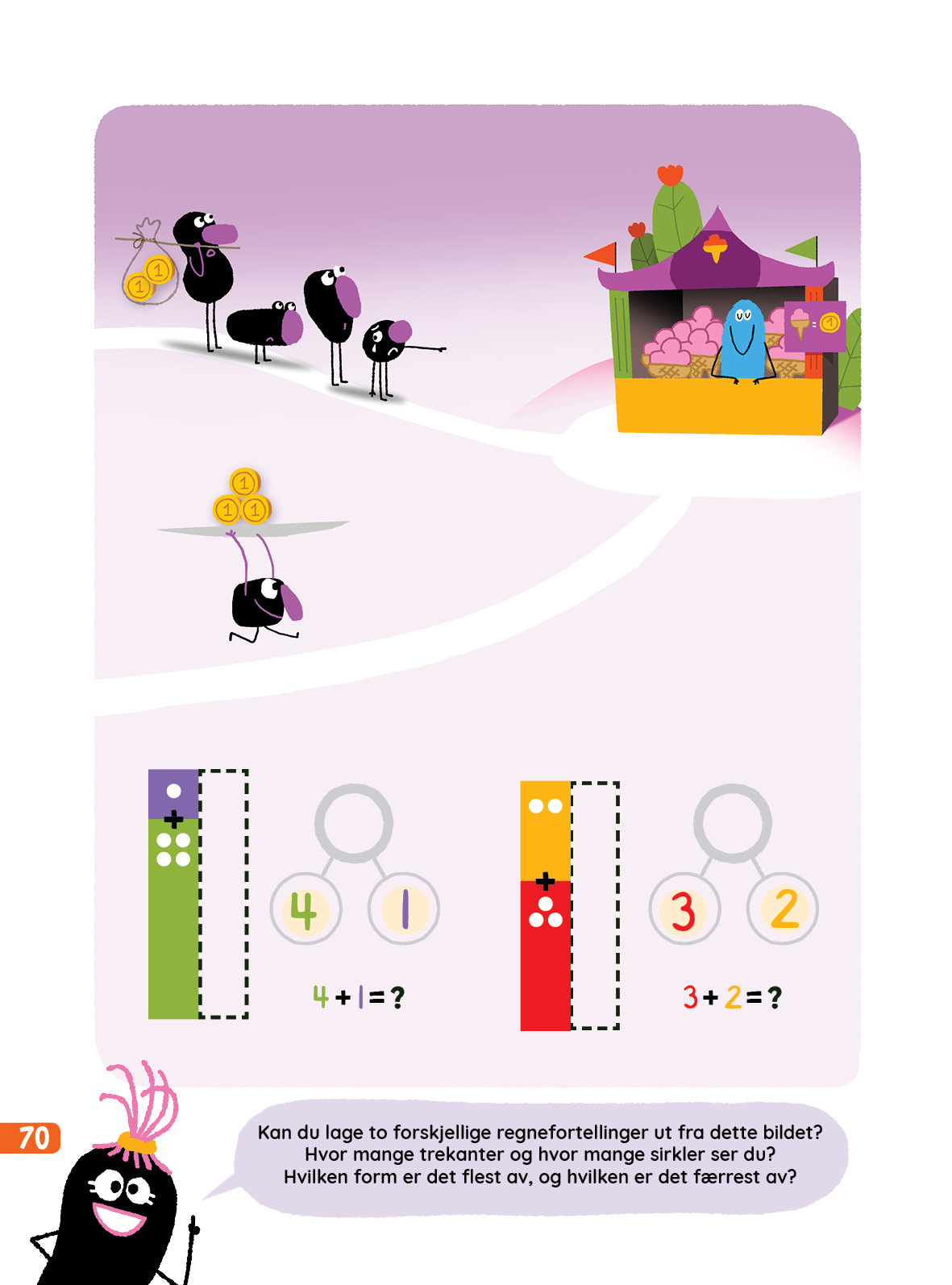
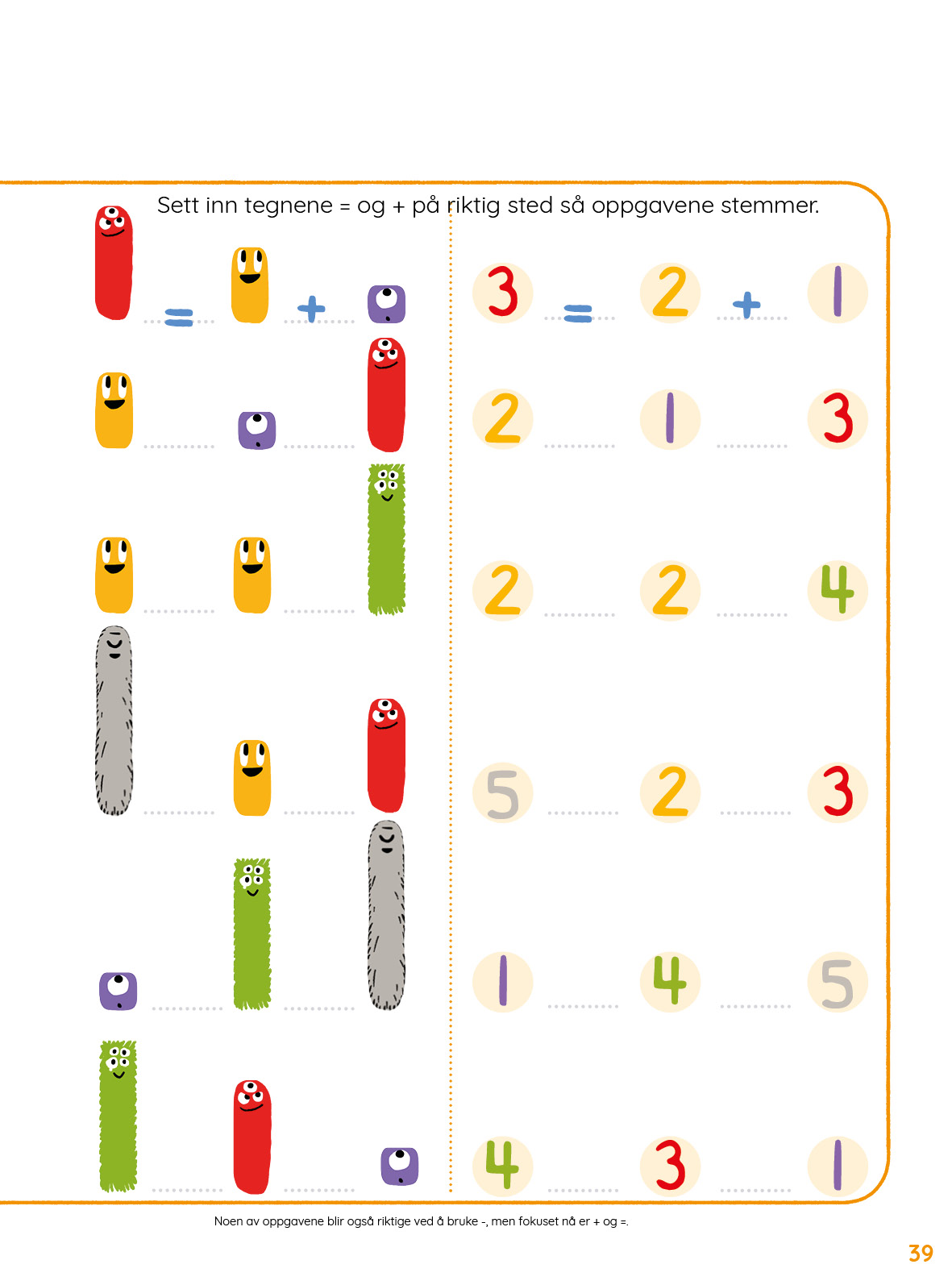
Denne uka skal elevene jobbe mer med regnefortellinger om addisjon. Disse skal gi en uformell introduksjon, så husk at vi fremdeles kun omtaler addisjon muntlig. Selve ”+”-tegnet introduseres med brask og bram i ukestema 9. Du kan lese mer om regnefortellinger under ”Lurt å vite” lenger ned på denne siden.
Økt 1 denne uka er som vanlig en repetisjonsøkt. Det er den usynlige noom og tallvenner som repeteres.
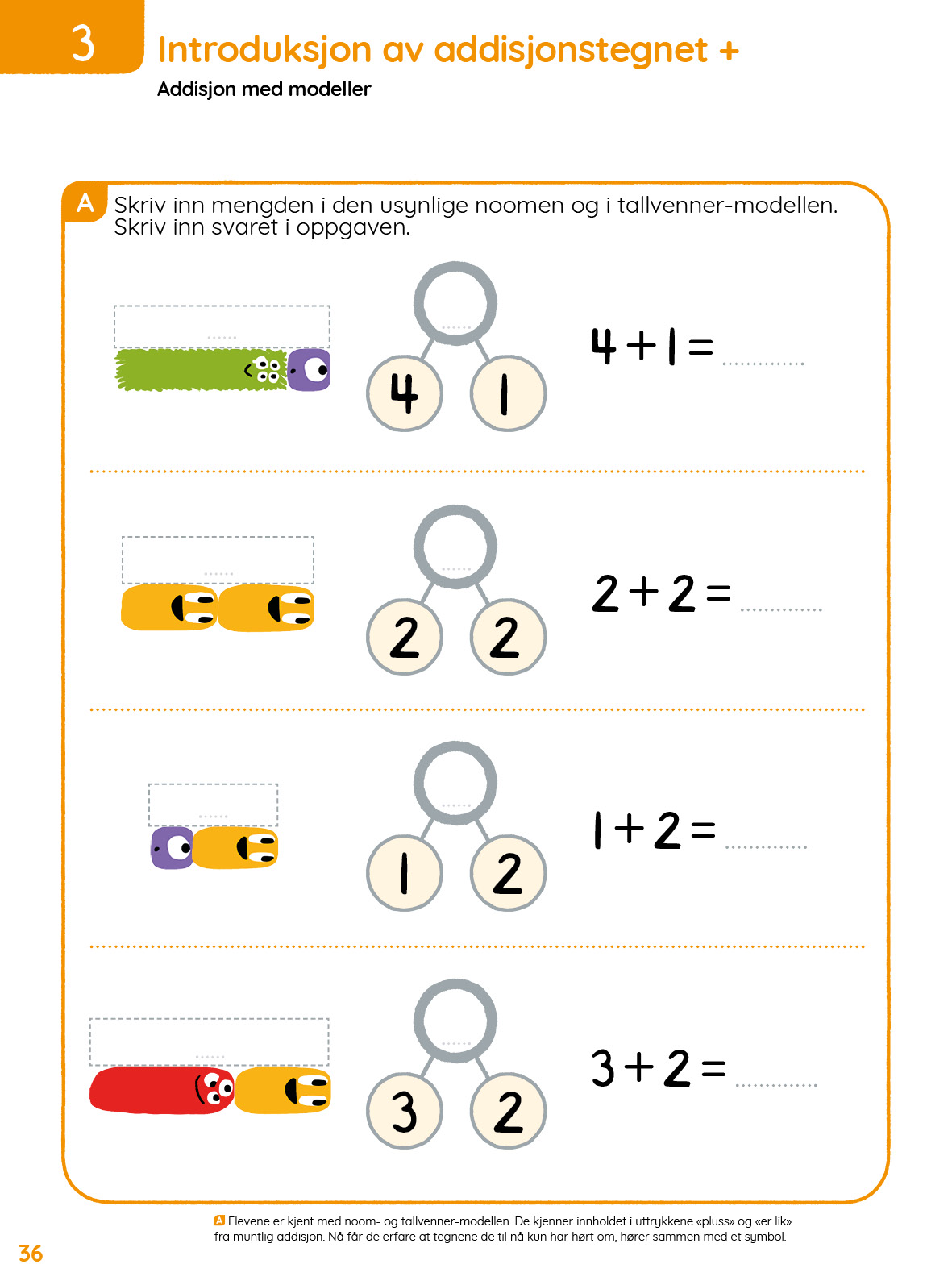
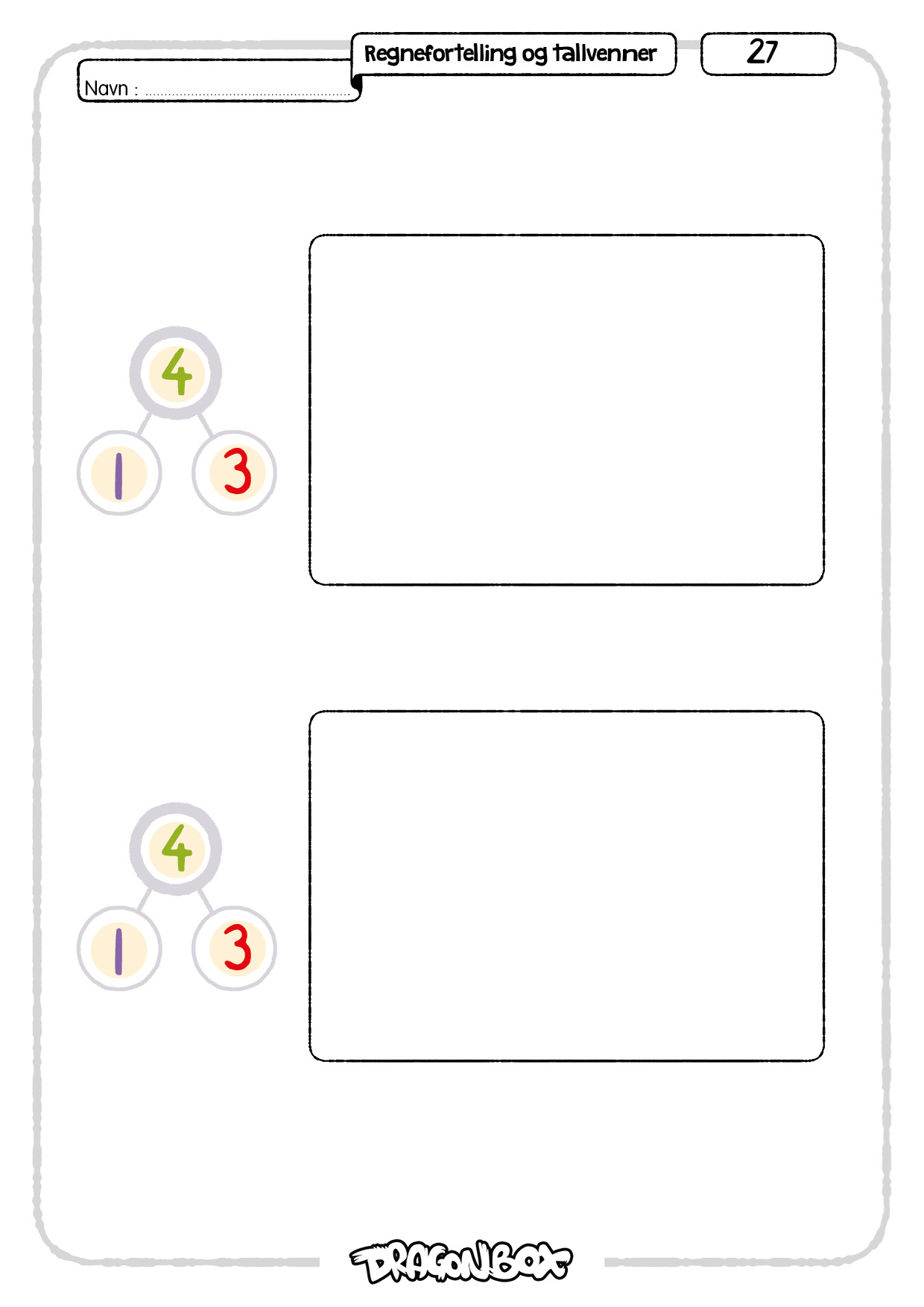
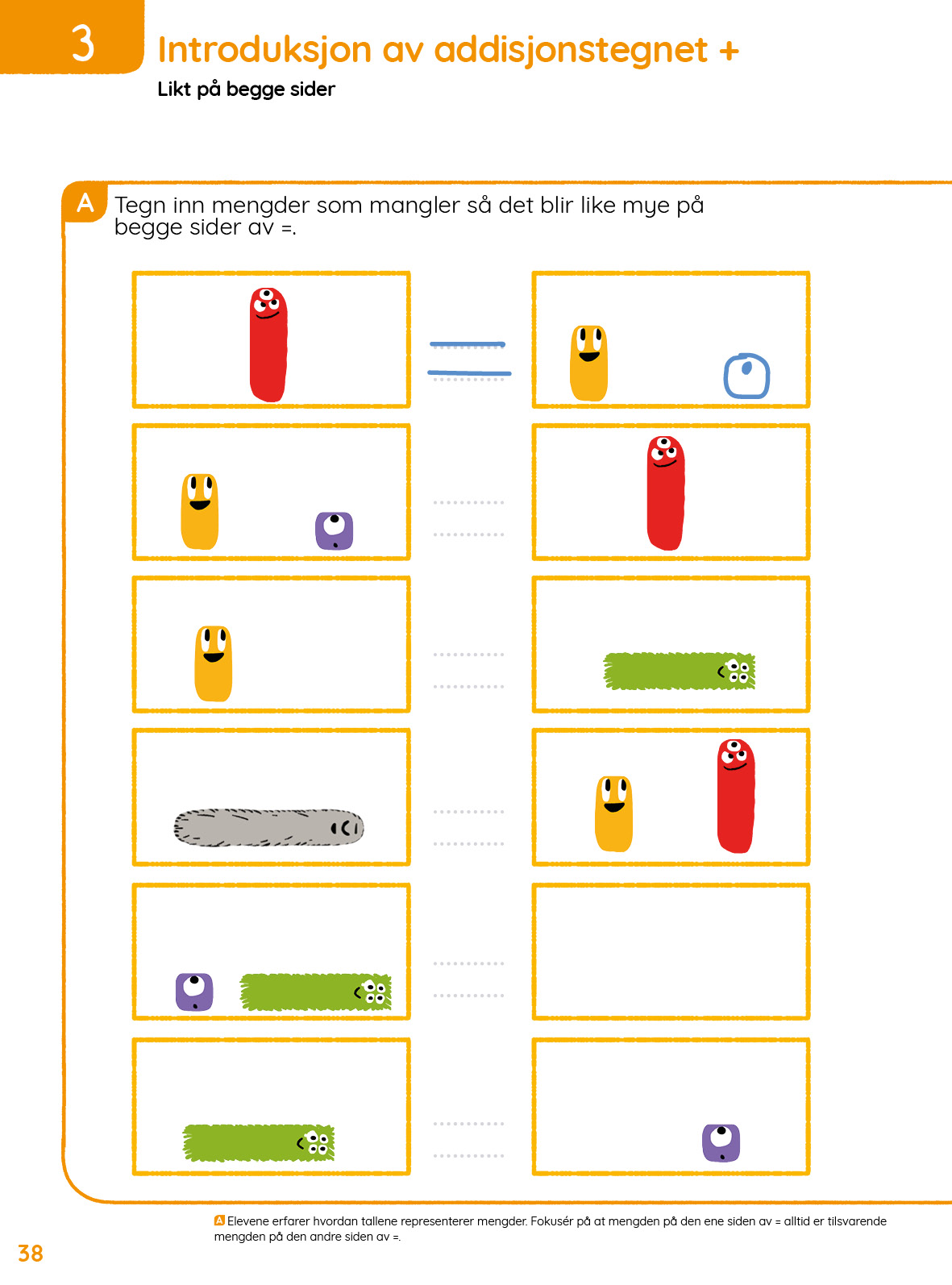
I økt 2 og økt 3 skal elevene knytte regnefortellinger sammen med tallvenner.
Den rike oppgaven i økt 4 handler om mønster. Vi ønsker at elevene skal øve seg på å lete etter mønster og beskrive det med egne ord, slik at de kanskje også begynner å lete etter mønster i addisjon og subtraksjon.
Lurt å Vite
Hjemmelekse
Vårt forslag:
- Mattesnakk side 68 (regnefortelling med fallskjerm) og side 70 (regnefortelling med is).
Fokus: Hvordan henger bilde-fortellingen sammen med tallvennene og noom-modellene. (Ikke "+"-tegnet eller likninger.)
Alternativer:
Mattestreker er fin å gi som lekse hvis det er sider der de ikke rekker på skolen. De som er ferdige med alt kan enten få kopiark eller nettbrettet med seg hjem.
Nettbrettene er fine å sende hjem som lekse. På nettbrettet kan de enten gjøre ferdig aktivitetene som hører til øktene denne uka, eller de kan spille DragonBox Numbers eller andre spill.
Økt 1: Repetisjon: den usynlige noomen og tallvenner
Mål
Elevene skal kunne:
- Visualisere mengder under 5 på forskjellige måter, med støtte i modell (tall, noomer, tallvenner).
Ekstra utstyr
Fokus
Beskrivelse
Økt 2: Uformell addisjon: sammenslåing med tallvenner og regnefortellinger
Mål
Elevene skal kunne:
- Lage enkel regnefortelling med addisjon, med støtte i bilde og modell (tallvenner).
Ekstra utstyr
Fokus
Beskrivelse
Økt 3: Uformell addisjon: sammenslåing med tallvenner og regnefortellinger
Mål
Elevene skal kunne:
- Tolke enkel regnefortelling med addisjon, med støtte i bilde.
Ekstra utstyr
Fokus
Beskrivelse
Økt 4: Rik oppgave: Tallmønster med noomer
Mål
Ekstra utstyr
- De fysiske noomene.
Fokus
Beskrivelse
Her kommer først en kort beskrivelse. For en utfyllende beskrivelse klikk i den gule boksen til høyre.

I denne oppgaven skal elevene fortsette et mønster. Målet med oppgaven er å få elevene til å beskrive mønsteret med egne ord. La elevene snakke og fortelle selv om ikke alt de sier er helt riktig. I siste del av oppgaven skal elevene lage egne mønster.
Det er viktig å huske på at et mønster kan fortsettes på uendelig mange måter, så det finnes egentlig ikke fasitsvar.
 Rik oppgave: Tallmønster med noomer
Rik oppgave: Tallmønster med noomer


Denne oppgaven handler om tallmønster med noomer. Målet er at elevne skal prøve å beskrive mønstrene med egne ord.
Det er viktig å huske på at et mønster kan fortsettes på uendelig mange måter, så det finnes egentlig ikke fasitsvar.
Introduksjon av oppgaven:
Legg et enkelt mønster med noomene, for eksempel dette:

Du kan bruke fysiske noomer, utklippede noomer med magneter bak, øvingslab på smartboarden eller tegne på ei tavle.
Snakk litt løst med elevene om hva neste tall i mønsteret kan være.
Lav inngangsterskel:
Del elevene i par og be dem fortsette mønsteret. Etter hvert kommer de til å gå tomme for de noomene de trenger. Dette er bare fint for det gir dem muligheten til å bygge noomene av mindre noomer/andre noomer enn de først hadde tenkt.
Gode spøsmål å stille:
Hvordan kan man vite hva neste tall i mønsteret skal være?
Hva er regelen i mønsteret.
Hva er tall nummer 10 i mønsteret?
Hvor langt kan vi bygge mønsteret?
Neste nivå:
Vis andre mønster til elevene som de kan fortsette. La elevene få jobbe litt med et mønster før du ber noen av dem forklare hva som er regelen. Under kommer noen forslag til mønster.
I denne oppgaven er det gode muligheter for individuell tilpasning fordi mønstrene kan ha mange ulike vanskelighetsgrader.
Del gjerne klassen i 4 grupper, og la parene i en gruppe jobbe med en annen vanskelighetsgrad en parene i en annen gruppe. Hvis de parene som jobber med samme mønster jobber i nærheten av hverandre så gir det også rom for gode diskusjoner parene i mellom. Når læreren så stiller spørsmål så kan dette gjøres gruppe for gruppe. På denne måten for gruppen god tid til å forklare det mønsteret de har jobber med.
GANSKE ENKELT
- Partalls-mønster:

- Oddetalls-mønster:

LITT VANSKELIG
- Telle med 3:

VANSKELIG
- Positive og negative tall:

- Mønster som vokser i lengde og bredde (2 dimensjoner).

Dette er et mønster med kvaderattallene (12, 22, 32 osv). Det er selvfølgelig ikke forventet at elevene skal kunne multiplikasjon og potenser, men antagelig er det noen elever som likevel kan beskrive mønsteret på sin egen måte.
Gode spørsmål til dette mønsteret kan være:
- Hvor mange 4'ere er det i neste tall? (4)
- Hvor mange 1'ere er det i neste tall? (4x4=16)
- Hvor mange 5´ere trenger dere for å lage tall nummer 5? (5)
- Hva heter tall nummer 5? (5x5=25)
- Hva er regelen for mønsteret?
- Hvilke noomer og hvor mange av dem trenger dere for å lage tall nummer 10? (10x10)
VELDIG VANSKELIG
- Mønster som vokser i lengde, bredde og høyde (3 dimensjoner).

Dette er et mønster med kubikktalleene (13, 23, 33 osv). Som over er det kun meningen at elevene skal prøve å beskrive mønsteret med sine egne ord, for eksempel (det vokser med 1 i alle retninger/overalt).
Gode spørsmål til dette mønsteret kan være:
- Hvor mange 4'ere er det i neste tall? (4x4, men elevene kommer nok til å si 4+4+4+4)
- Hvor mange 1'ere er det i neste tall? (4x4x4=64)
- Hva er regelen for dette mønsteret?
- Hvor mange 5´ere trenger dere for å lage tall nummer 5? (5x5)
- Prøv å finne ut hva tall nummer 5 heter. (5x5x5=125)
- Hvordan Kan dere lage tall nummer 10? (10x10x10=1000)
Åpen utgang:
La elevene lage egne mønster som enten læreren eller andre elever skal fortsette. La gjerne mønstereieren selv få fortelle hvorvidt den andre klarte å fortsette mønsteret slik de hadde tenkt. Hvorfor/hvorfor ikke? Forklar regelen i mønsteret.