Tema 4: Tallene 0-5: den usynlige noom
Mål
Elevene skal kunne:
- Knytte sammen mengder under 5, til riktig tall.
- Forklare med egne ord at like mengder kan visualiseres på ulike måter. (Eks: Tri, tre prikker, tallet tre, tre Uno osv..)
- Med støtte i modell (noomer), forklare at den totale mengden (summen) er den samme uavhengig av rekkefølgen tall adderes i.
Fokus
Denne uka fortsetter arbeidet fra forrige uke med å forestille seg oppgaver. Helt konkret introduseres den usynlige noom i økt 2, og elevene skal forestille seg hvor mange enere denne består av. Du kan lese mer om den usynlige noom under ‘Lurt å vite’ på denne siden.
Det er mange uker til vi skal begynne med addisjon og subtraksjon. Vi ønsker likevel at du fra denne uka muntlig begynner å bruke ord som ‘pluss’ og ‘minus’ når du snakker. Dette vil være med å skape en begynnende intuisjon hos elevene om operasjonene addisjon og subtraksjon, og det vil hjelpe dem når de senere skal formalisere begrepene.
Når en noom spiser en annen kan man bruke ordet ”pluss” istedenfor ‘spise’. For eksempel så kan man si ‘2 pluss 3 blir 5’ når noomene 2 og 3 spiser hverandre. Det samme gjelder for ”minus”: Hvis vi har en 5’er noom og kutter av en 1’er, så kan man si ‘5 minus 1 er 4’.
Økt 1 er også denne uka en repetisjonsøkt. Elevene får i denne økta repetert ulike tallrepresentasjoner fra forrige uke.
Økt 3 et første møte med kommutativitet og flerledds utrykk._ Kommutativitet_ er et matematisk begrep som viser til at 2+3 er det samme som 3+2. Du kan lese mer om kommutativitet under ‘Lurt å vite’ på denne siden. Flerledds uttrykk betyr at vi har mer enn to ledd i uttrykket. For eksempel så kan vi ha en 1’er noom, en 2’er noom og to 1’er noomer over hverandre. Dette omtales om ”1 pluss 2 pluss 1 pluss 1”.

Økt 4 denne uka handler om tallvenner. Hvis du ikke har kommet i gang med rike oppgaver ennå, anbefaler vi å gjøre den rike økta denne uka fordi den bygger opp mot det som kommer i neste uke.
Lurt å Vite
DEN USYNLIGE NOOM

Den usynlige noom er rett og slett en gjennomsiktig/usynlig noom som kan gjøres høyere og lavere ved å dra i den hvite pilen på toppen av den.
Matematisk så representerer den usynlige noom den ukjente delen i en likning. Ved å sette sammen vanlige noomer sammen med den usynlige noom (som på bildene under), får man en visuell modell av addisjon og subtraksjon.

Når den usynlige noomen representerer helheten (bildet over), så har vi en modell for addisjon.

Når den usynlige noomen representerer en av delene (bildet over), så har vi en modell for subtraksjon.
Når elevene jobber med den usynlige noom er det viktig å tenke både lengder og enere. Oppgaven er å prøve å forestille seg hvor mange enere det er i den usynlige noom uten å telle på den.
KOMMUTATIVITET
Kommutativitet er en matematisk egenskap som gjelder for to av de fire regneoperasjonene som man jobber med i grunnskolen (addisjon og multiplikasjon).
Kort sagt betyr kommutativitet at man kan endre på rekkefølgen uten at svaret endres. For addisjon betyr dette at 5+2 er det samme som 2+5. Det er viktig å jobbe med dette med elevene, slik at de etterhvert kan forenkle regneprosessene: Hvis de vet at 5+2 er 7, vet de samtidig at 2+5 er 7.
Det er også viktig å jobbe med at subtraksjon ikke er kommutativ. 5-2 er som kjent ikke det samme som 2-5.
Hjemmelekse
Denne uka kan det være fint å sende hjem kopiark med tallkriving som lekse.
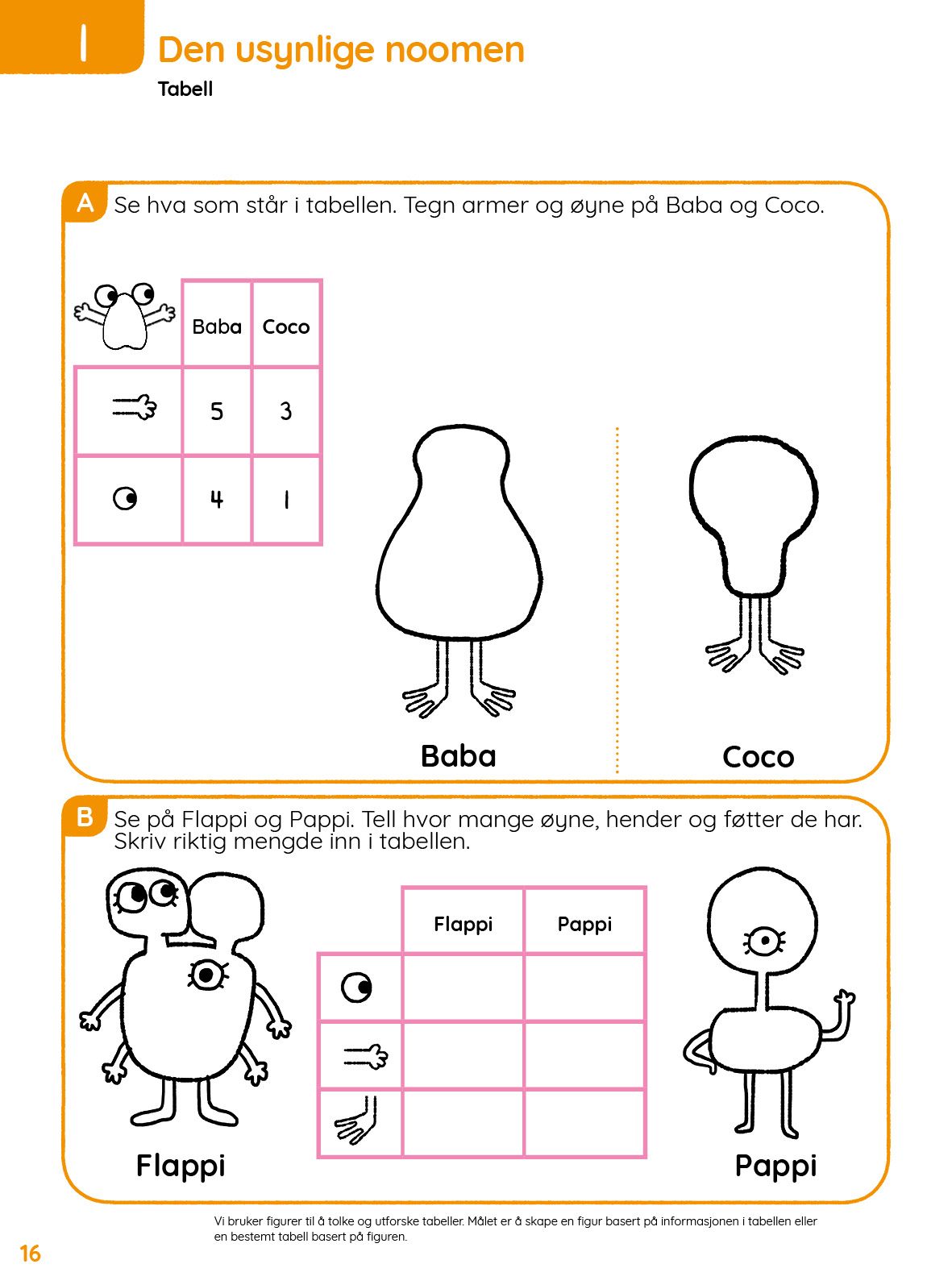
Økt 1: Repetisjon: ulike representasjoner
Mål
Elevene skal kunne:
- Knytte sammen mengder under 5, til riktig tall.
Ekstra utstyr
Fokus
Beskrivelse
Økt 2: Den usynlig noom
Mål
Elevene skal kunne:
- Forklare med egne ord at like mengder kan visualiseres på ulike måter. (Eks: Tri, tre prikker, tallet tre, tre Uno osv..)
Ekstra utstyr
Fokus
Beskrivelse
Økt 3: Flere ledd og kommutativitet
Mål
Elevene skal kunne:
- Med støtte i modell (noomer), forklare at den totale mengden (summen) er den samme uavhengig av rekkefølgen tall adderes i.
Ekstra utstyr
Fokus
Beskrivelse
Økt 4: Rik oppgave: Tallvenner
Mål
Elevene skal introduseres for og forberedes på tallvenner som kommer i neste uke.
Ekstra utstyr
Kopiarkene som du finner til høyre.
Kopiark 17-19: Disse er i farger og må printes i farger. Vi anbefaler å printe noen ekstra slik at de som synes det er litt vanskelig kan gjøre samme kopiark flere ganger.
Kopiark 20-25: Disse kan printes i svart/hvitt.
Kopiark 26: Dette printes også i svart/hvitt. Vi anbefaler å printe ekstra av dette arket da det kan brukes flere ganger og på mange forskjellige måter.
De fysiske noomstavene.
Fokus
Beskrivelse
Her kommer først en kort beskrivelse. For en utfyllende beskrivelse klikk i den gule boksen til høyre.
Denne rike økta er en introduksjon til en modell for tallvenner. Elevene skal jobbe med oppgaver på ark som har ulike vanskelighetsgrader. Det siste arket kan gjøres på mange ulike måter og gir en åpen utgang på oppgaven.
 Rik oppgave: Tallvenner
Rik oppgave: Tallvenner

Denne rike økten handler om tallvenner.
Introduksjon av oppgaven:
Vi foreslår at du går gjennom noen oppgaver i plenum (samling) før elevene selv får sitte og jobbe med disse oppgavene på kopiark.
Lav inngangsterskel:
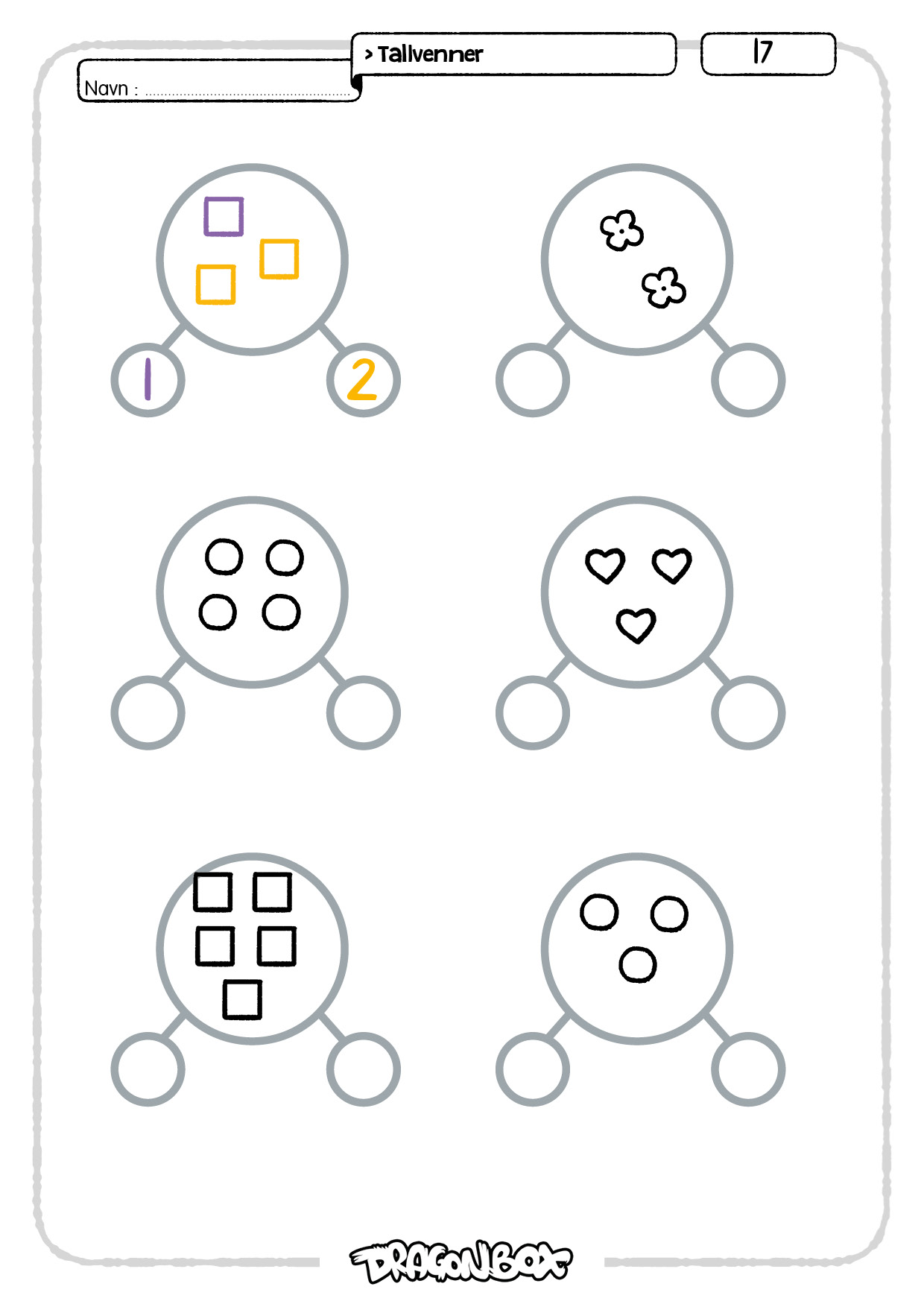
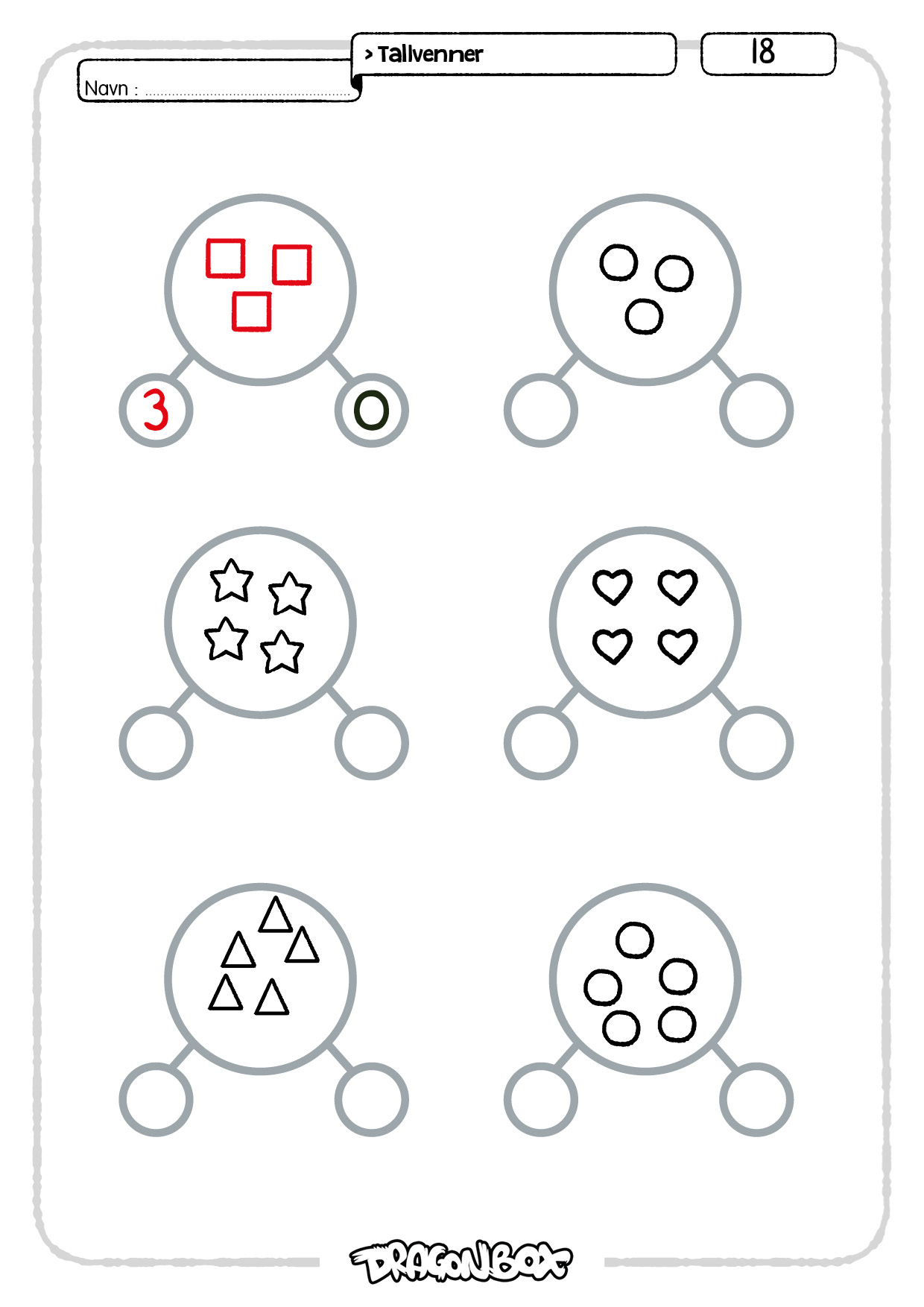
Ark 17-18.
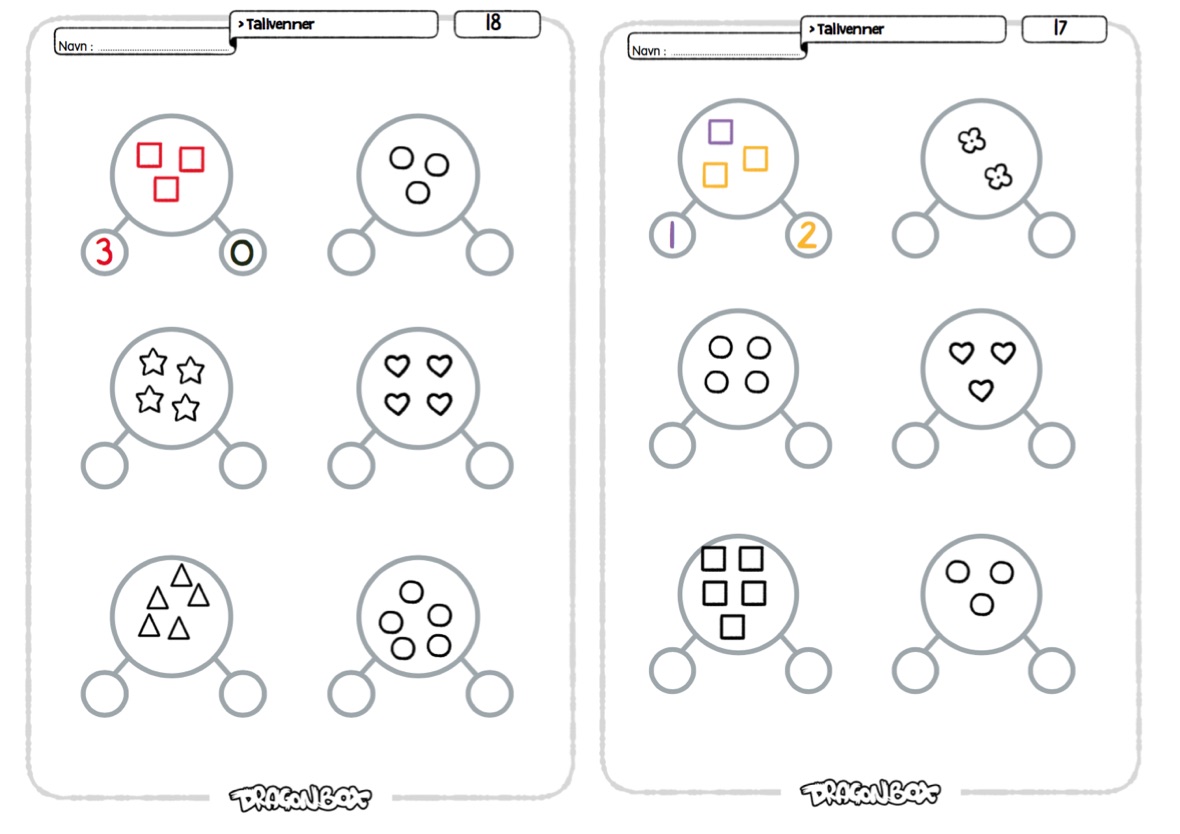
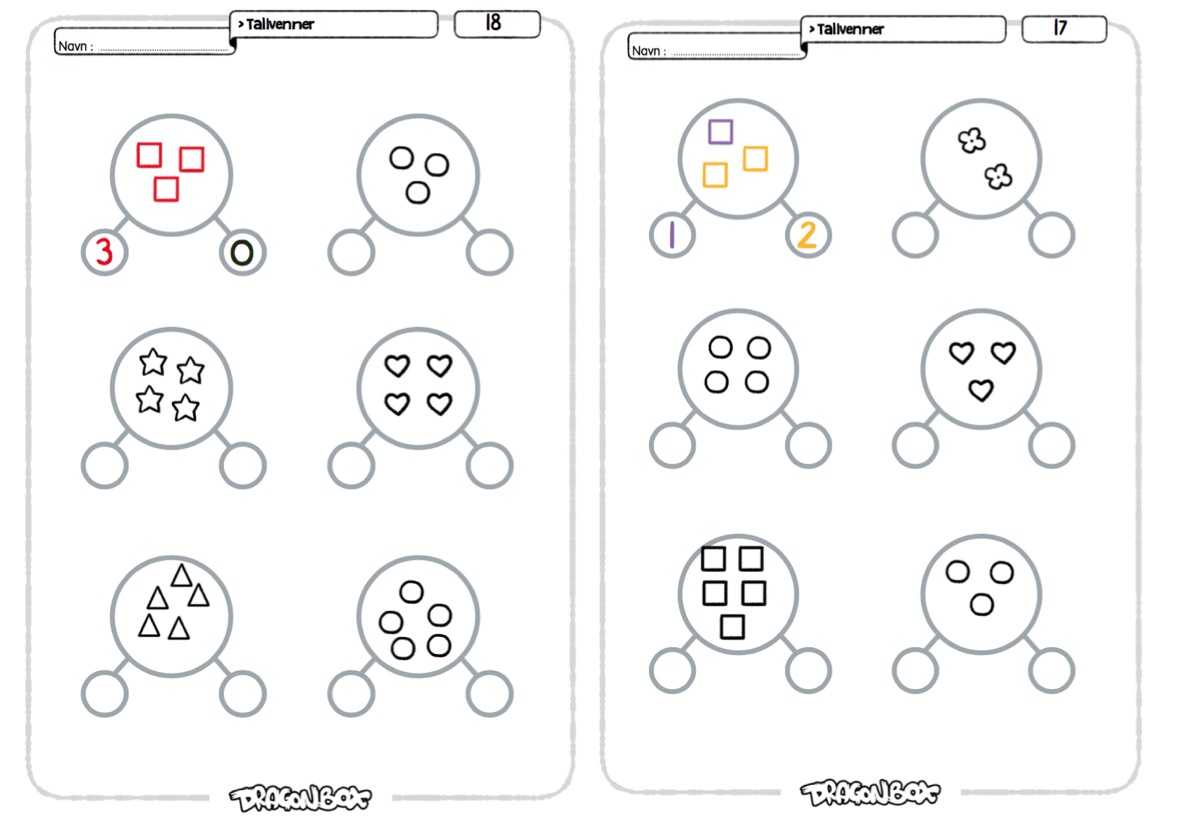
Her skal elevene dekomponere mengder ved å først fargelegge mengden med to farger slik at mengden blir delt i to, og deretter skrive dekomponeringen med tall.
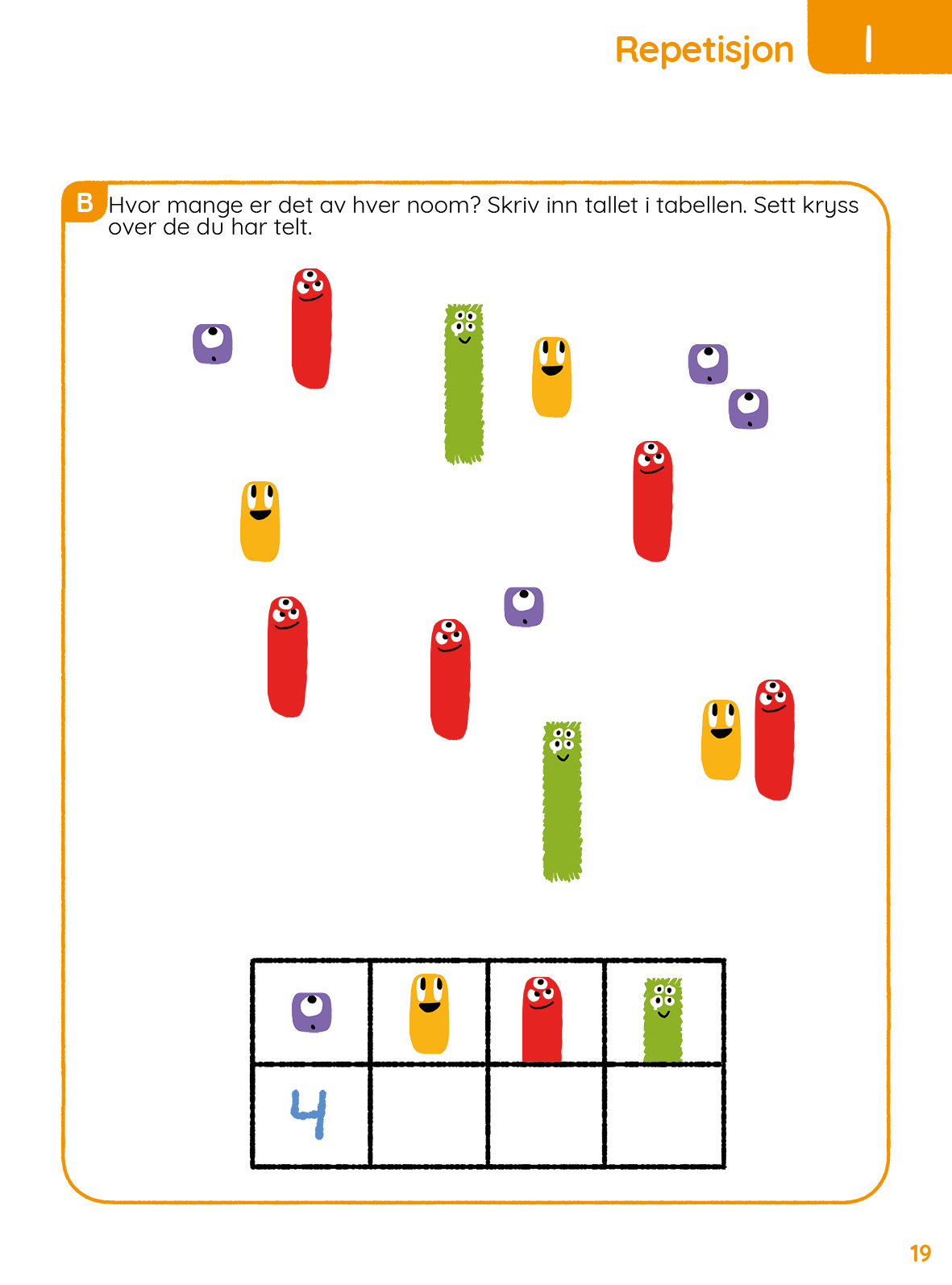
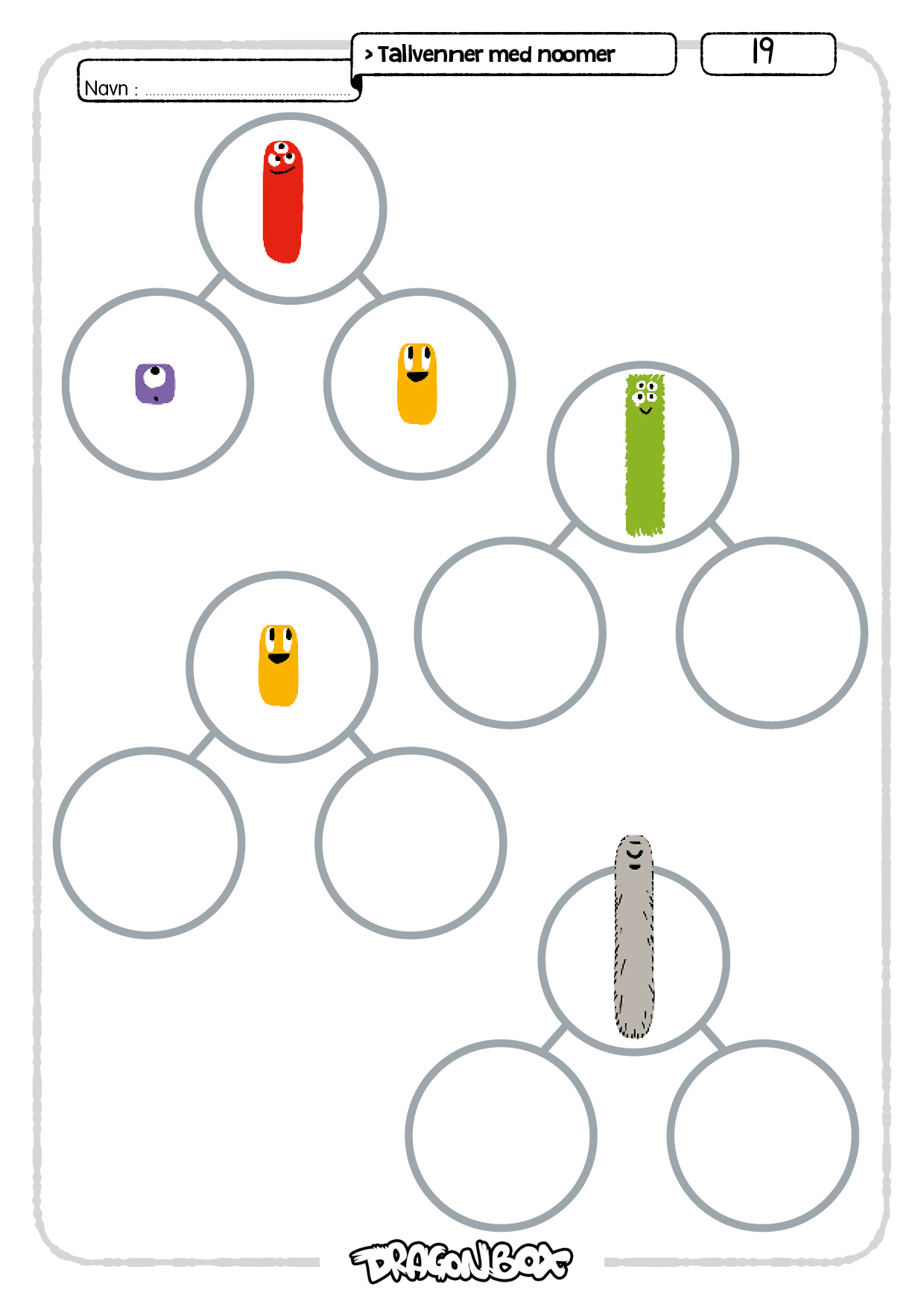
Ark 19.
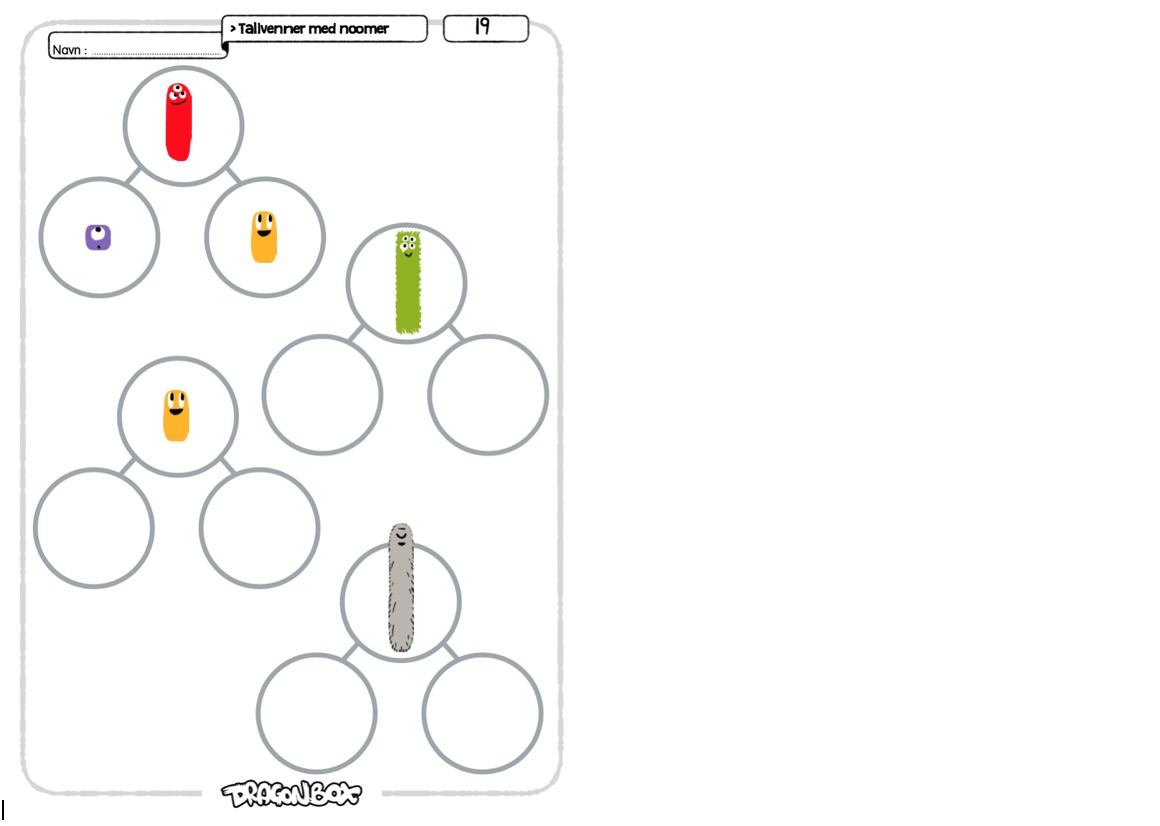
Her skal elevene dekomponere noomer. Elevene skal bruke fysiske noomstaver som hjelp på dette arket, slik at de har mulighet til å bruke noomstavene som hjelp på de vanskeligere oppgavene.
Elevene som synes disse oppgavene er litt vanskelige kan med fordel gjøre de samme arkene flere ganger.
Neste nivå:
På disse arkene skal elevene fylle inn tallene som mangler. Vi oppfordrer elevene til å bruke de fysiske noomstavene som hjelp slik at de får en større forståelse av hva de gjør.
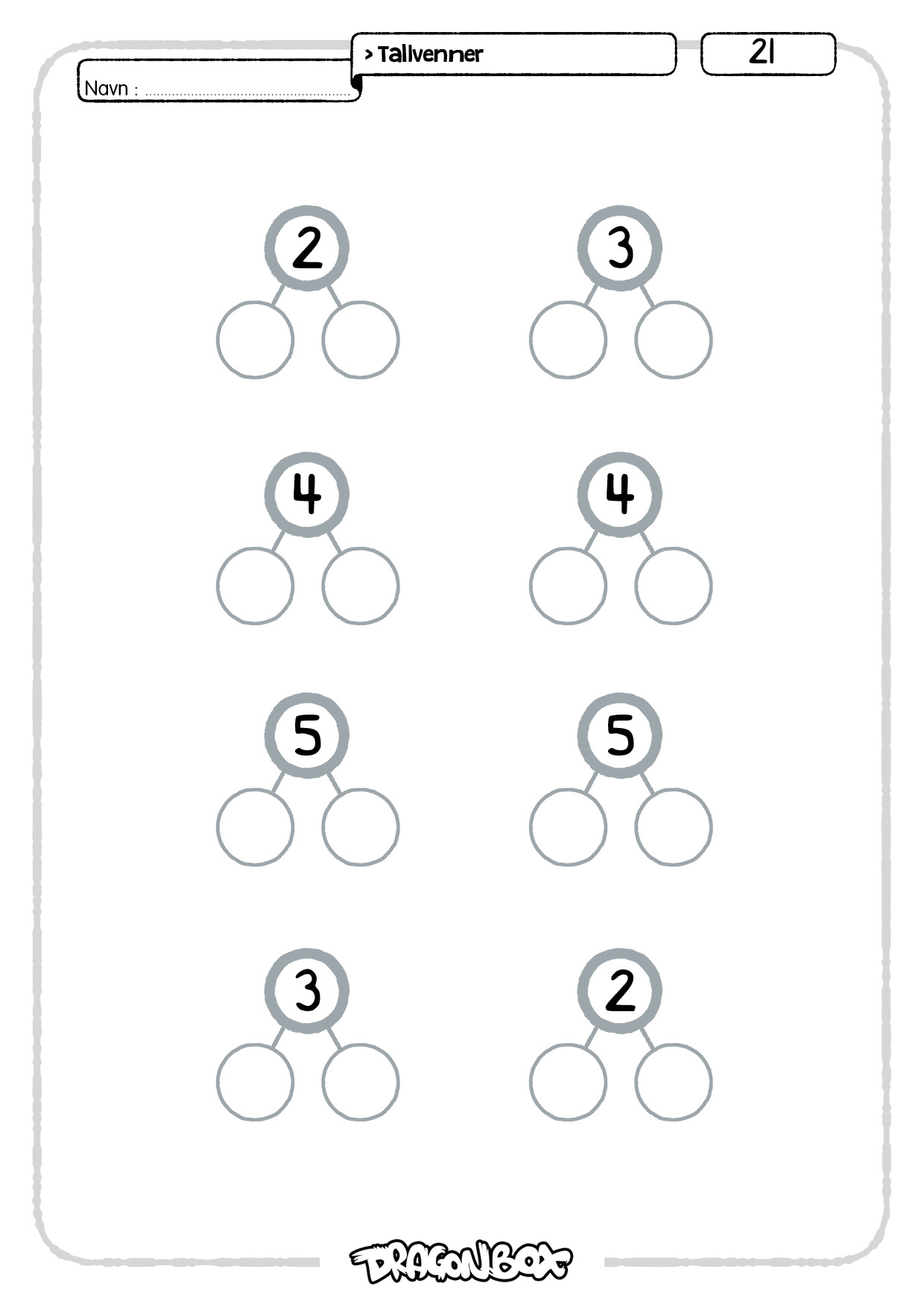
Ark 20-21.
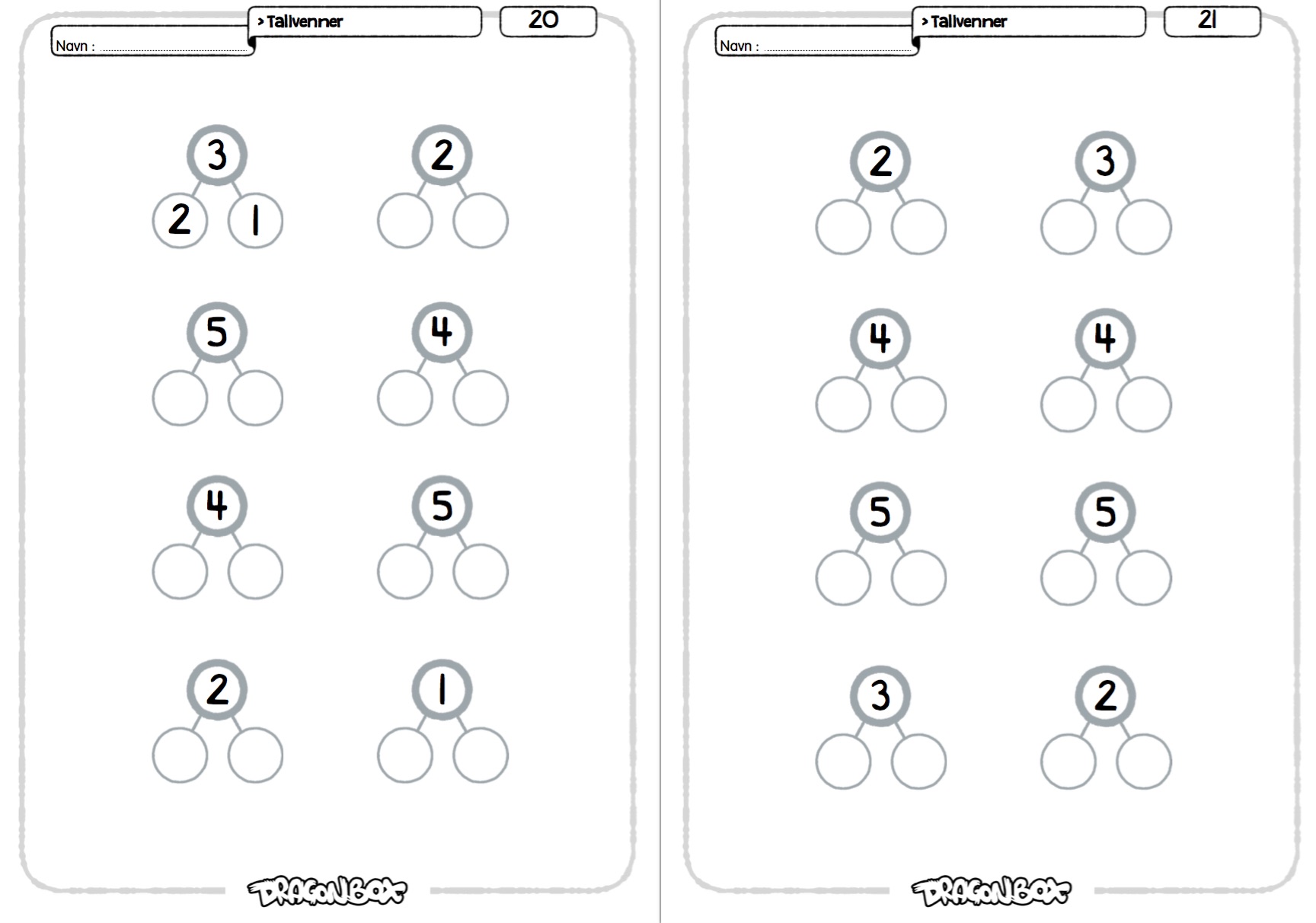
På disse to arkene skal man dekomponere tall. Man velger dekomponeringen selv.
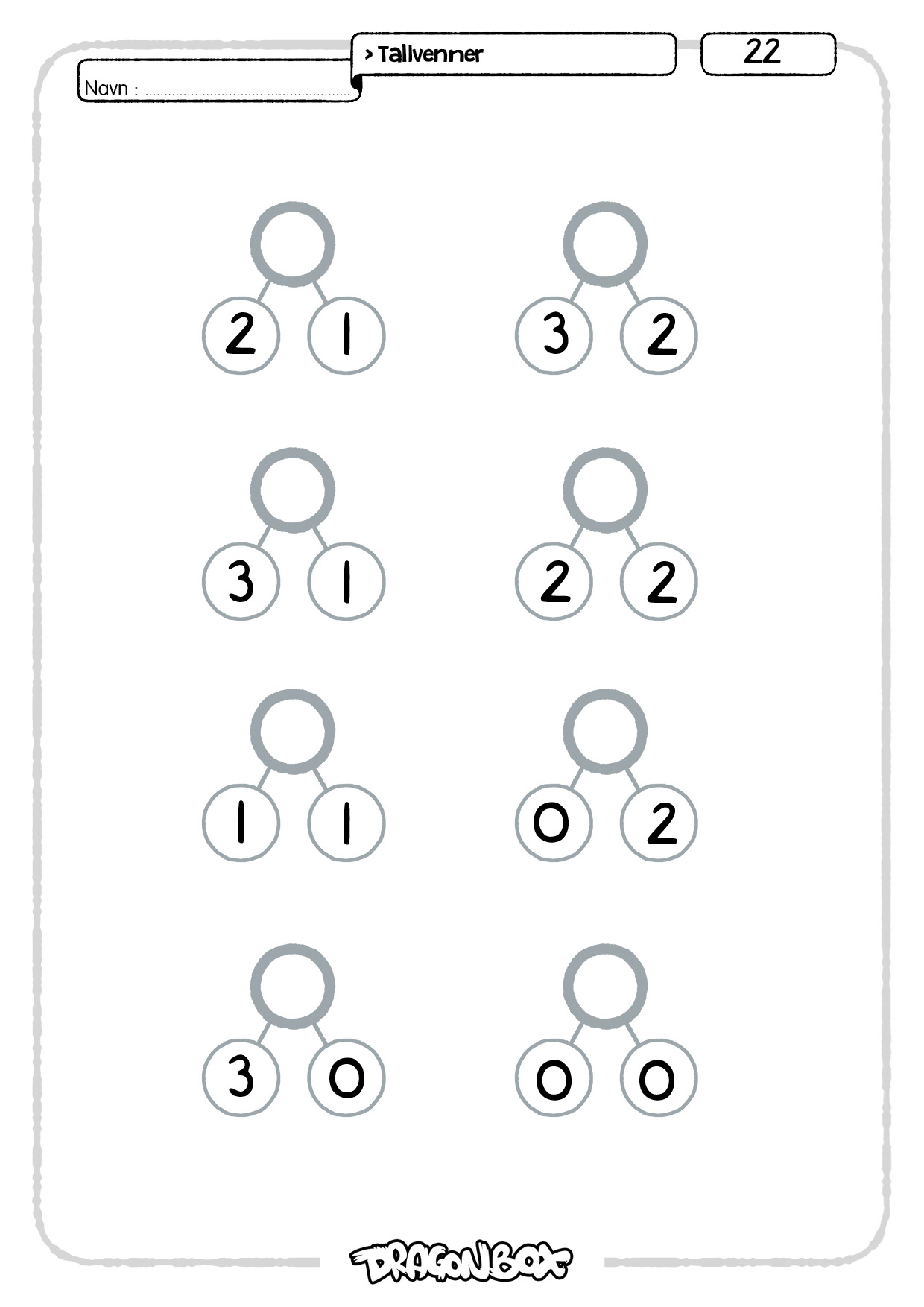
Ark 22-23.
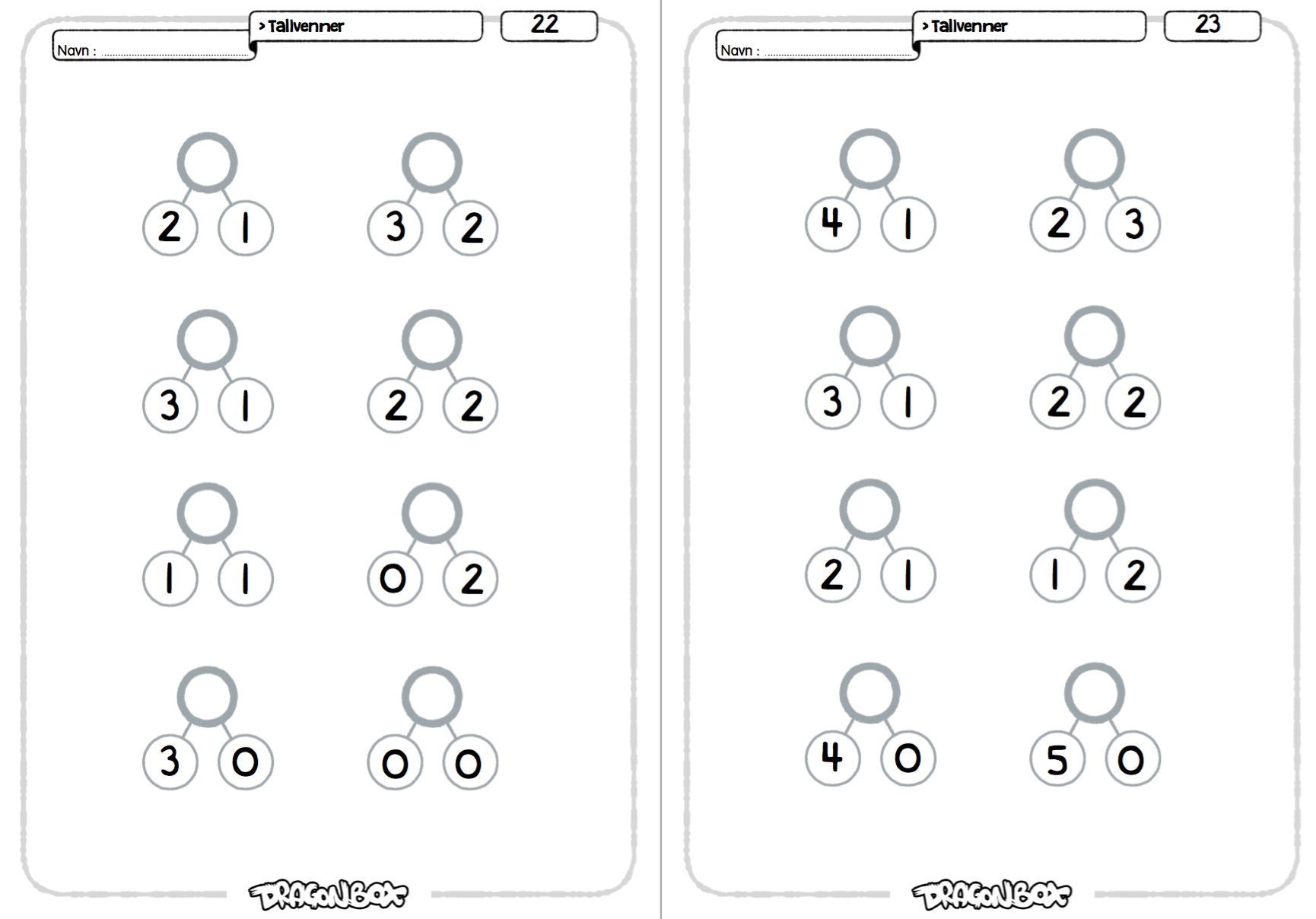
På disse to arkene skal man finne summen av de to tallene som er oppgitt.
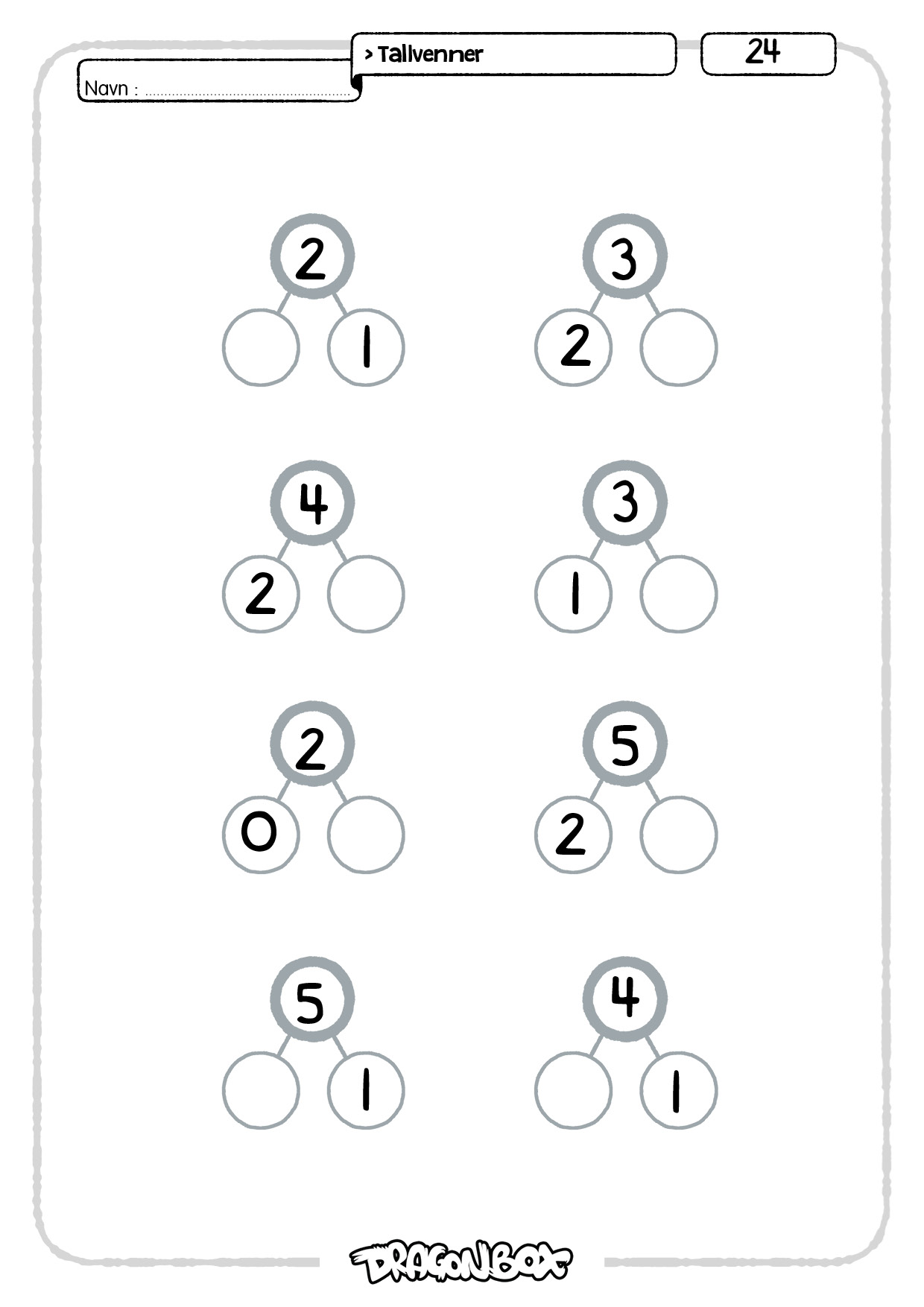
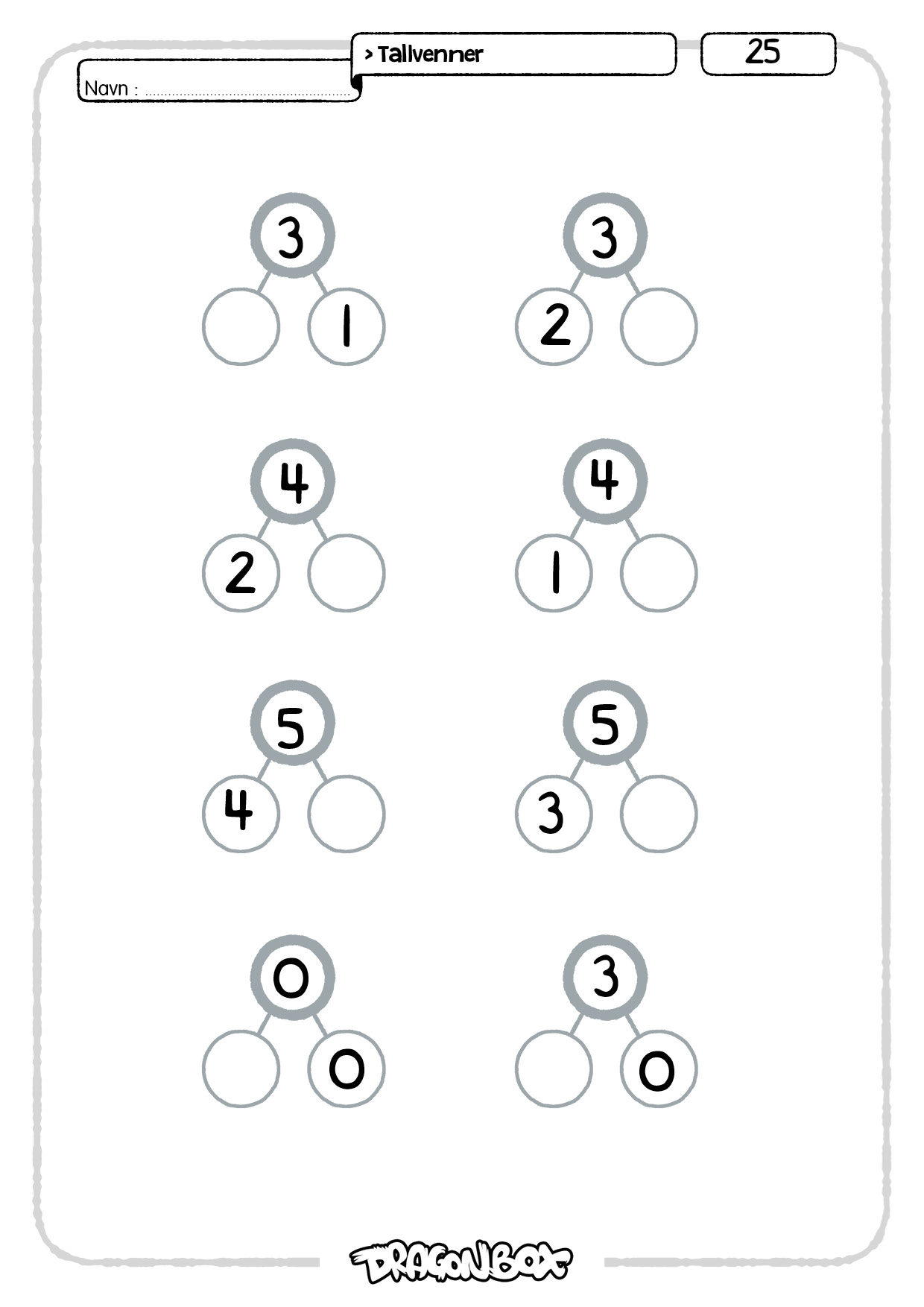
Ark 24-25.
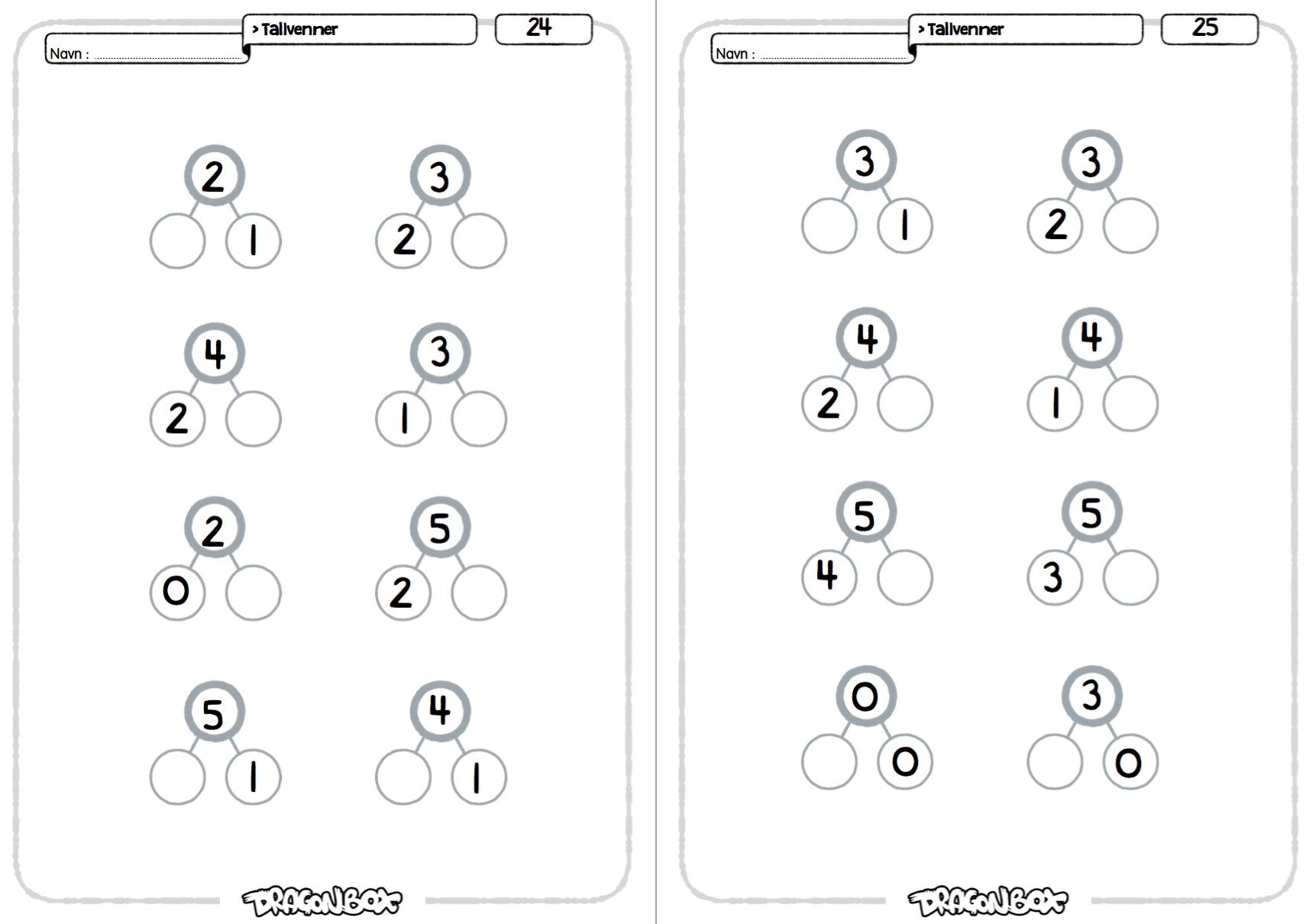
På disse to arkene skal man finne den ene ukjente delen når både helheten og den andre delen er gitt. Dette er et aller første steg i å kunne forestille seg subtraksjon.
Åpen utgang:
Ark 26.
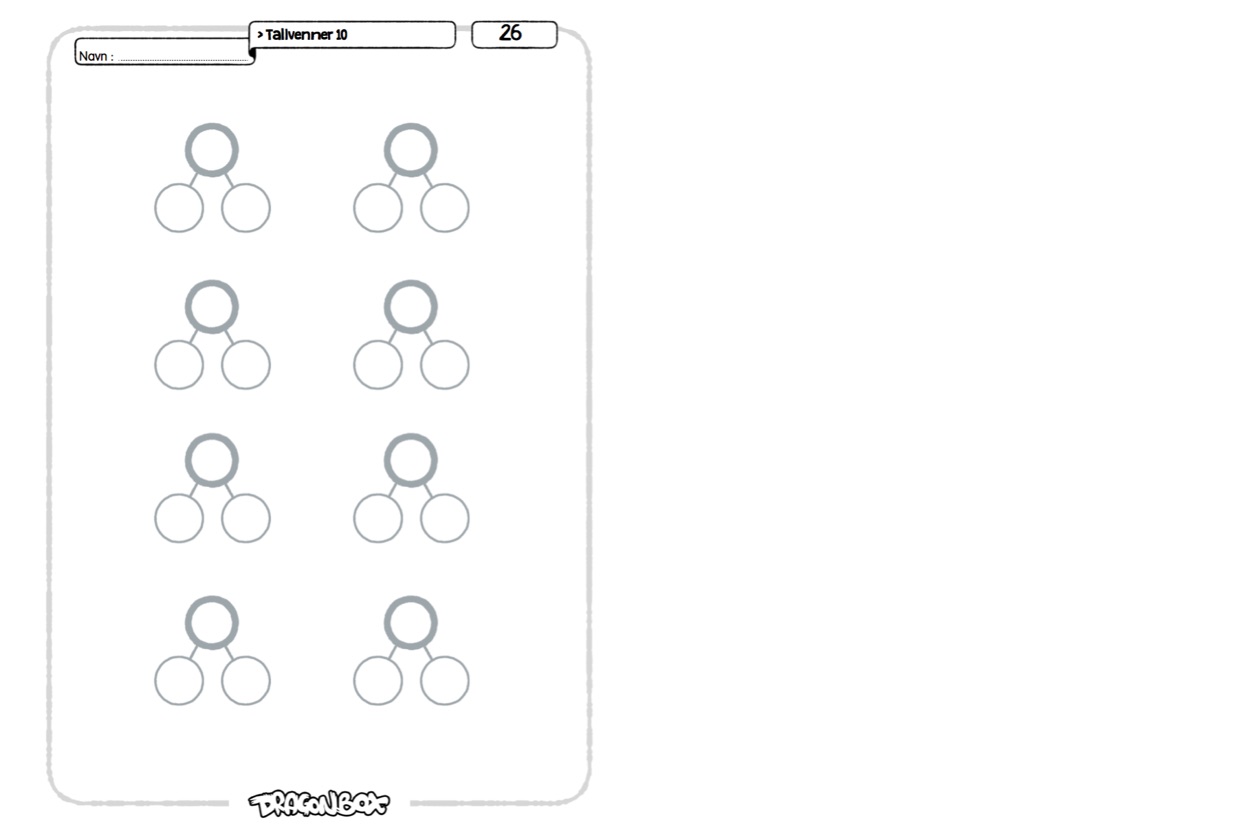
Dette arket kan brukes på forskjellige måter. Her er noen tips og eksempler, men føl deg helt fri til å velge andre måter å bruke dette på.
La elevene selv velge hvilke tall de skal dekomponere.
Be elevene velge samme ”helhet” i alle oppgavene, altså det tallet som står øverst i tallvenne-figuren. Be dem så undersøke hvor mange måter de kan dekomponere dette tallet/helheten i to deler. Hvordan vet elevene at de har funnet alle dekomponeringene?
Utfordre elevene på å velge høye tall, feks tall i området 11-20 eller enda høyere tall, for de elevene som mestrer det.
Bruk arket i par: Begge elevene fyller ut arket slik at en sirkel står tom i hver oppgave. Deretter bytter de ark om fyller inn det som mangler på den andre sitt ark.