Tema 3: Tallene 0-5: ulike tallrepresentasjoner
Mål
Elevene skal kunne:
- Tegne og gjenkjenne mengder opp til 5 med støtte i modell (enkelboks).
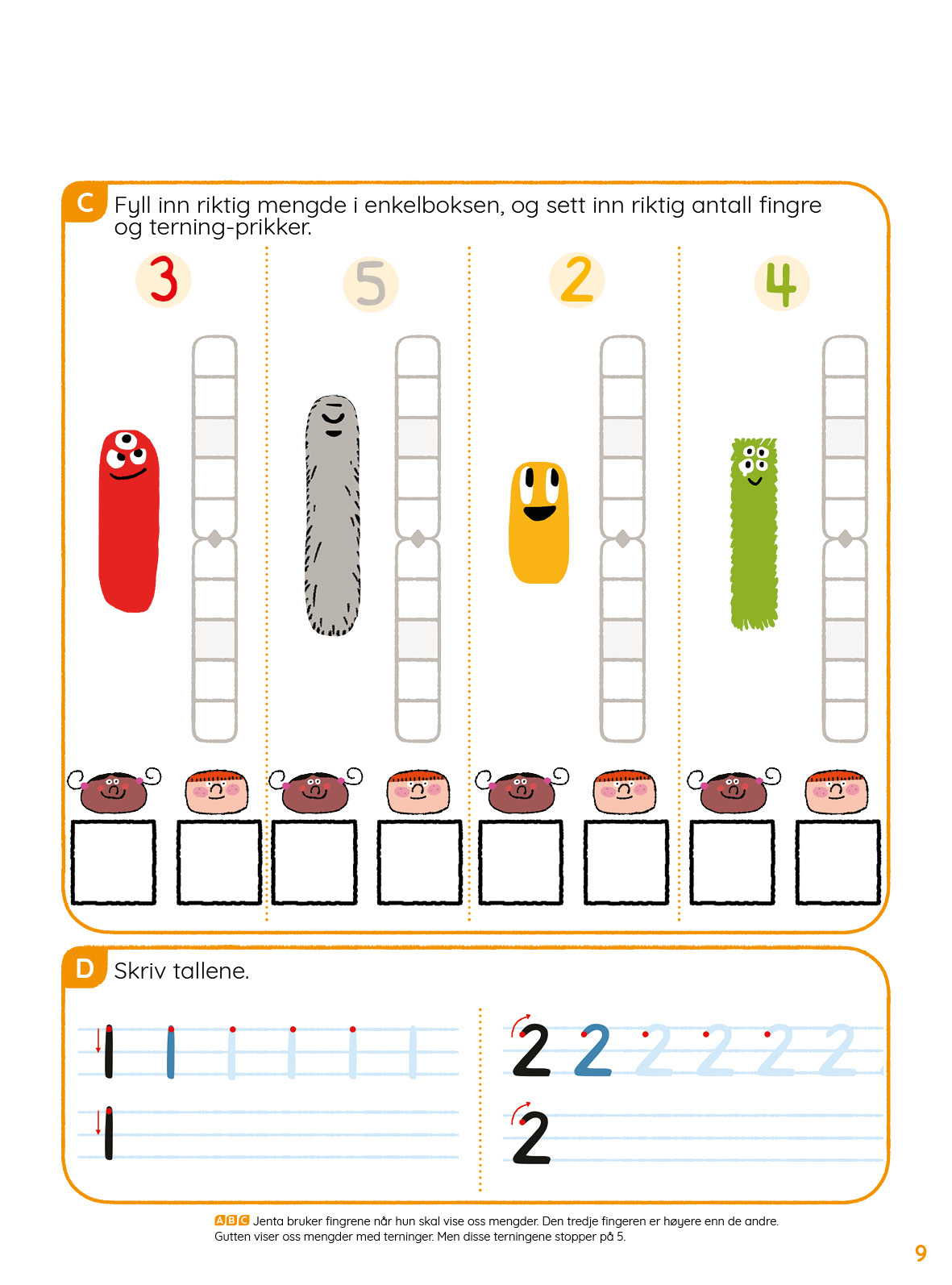
- Skrive tallene 0-5 med hjelpelinje.
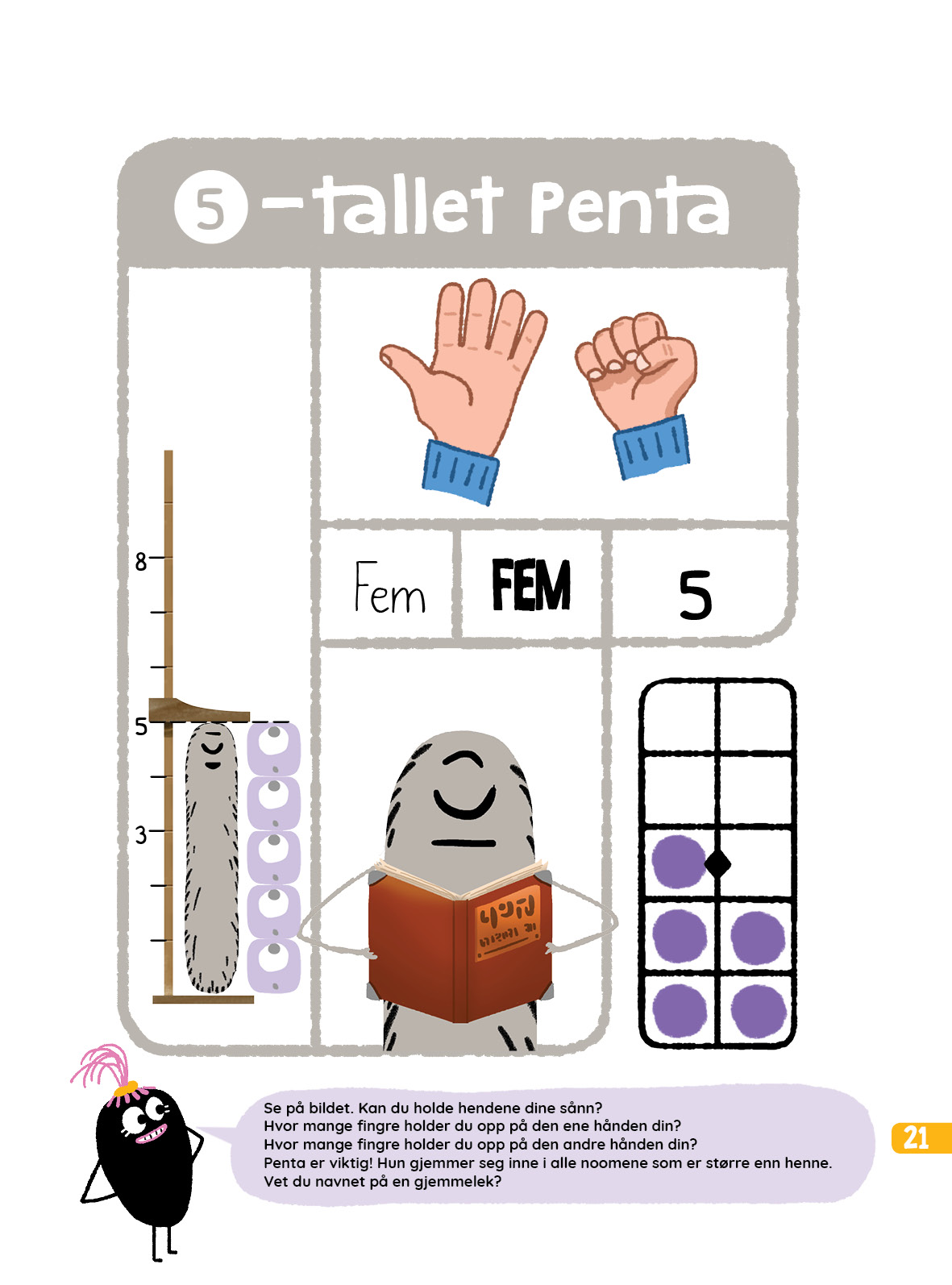
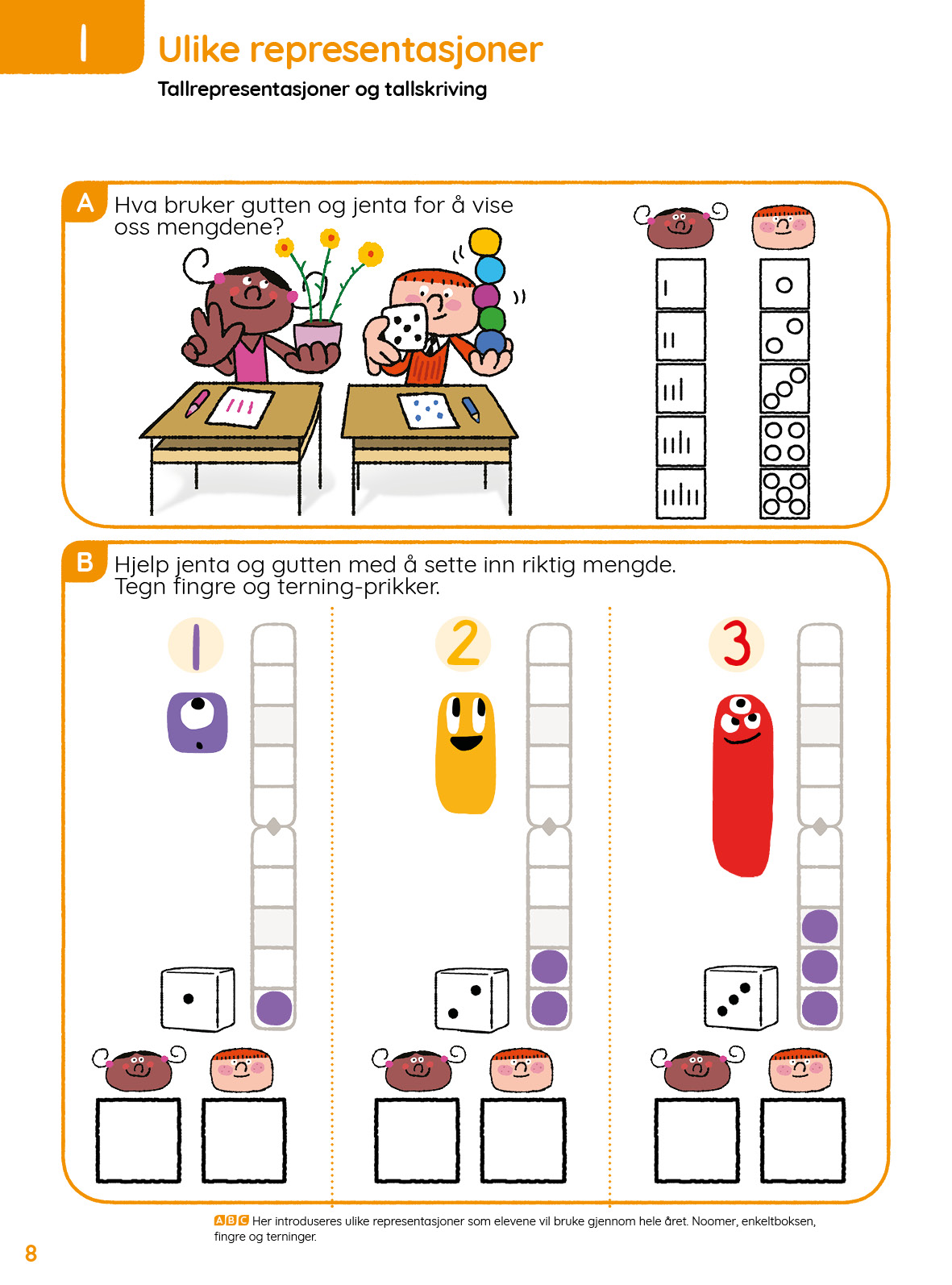
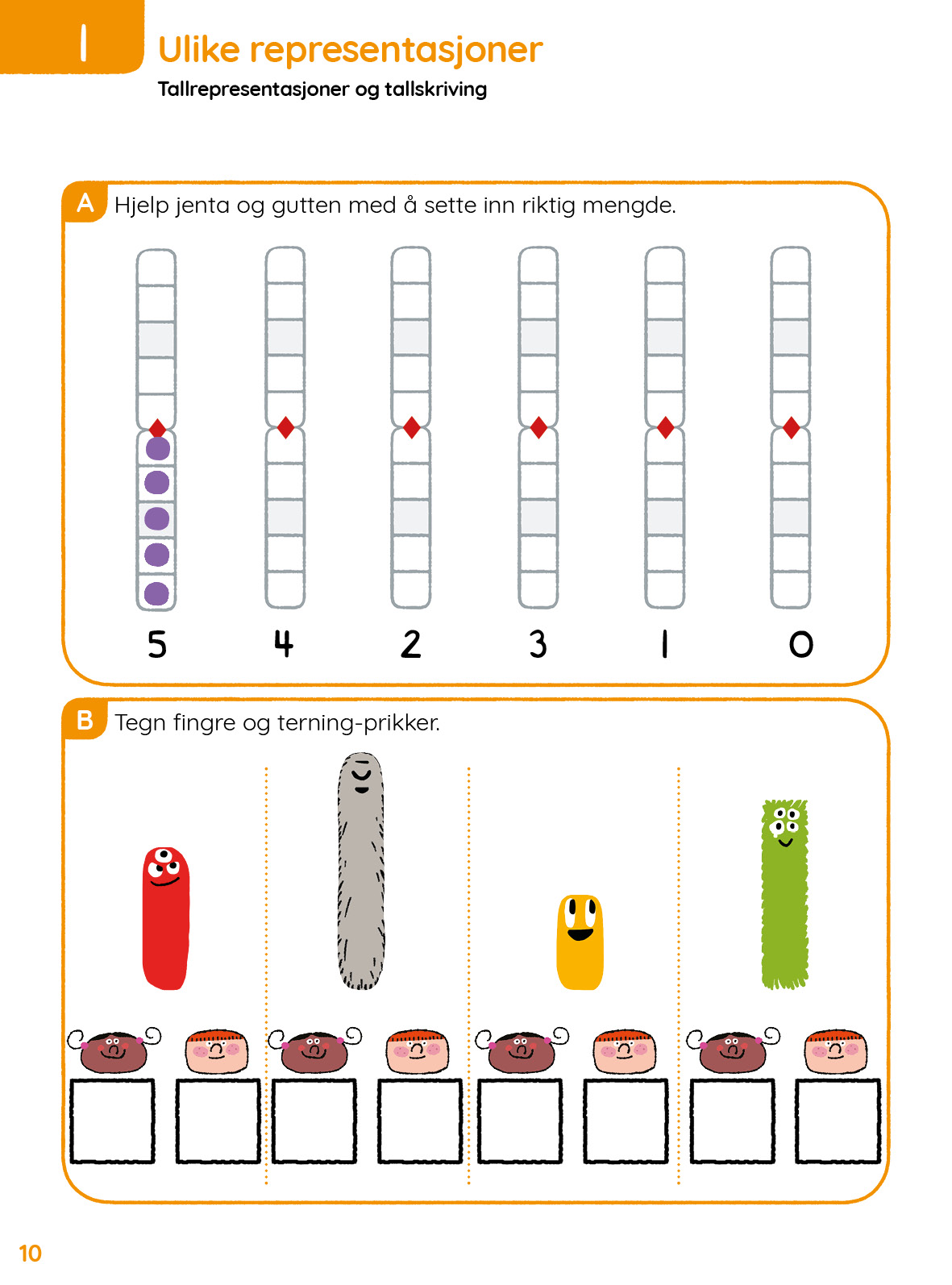
- Representere mengder under 5 på forskjellige måter (tall, noomer, enkelbokser, terninger, fingre).
- Lese av enkel tabell.
Fokus
Den første økta denne uka er en repetisjon av forrige uke. Elevene repeterer enkelboksen og tallskriving. I tillegg introduseres elevene for en ny type oppgave som vi kaller ”gardiner”. I disse oppgavene får elevene kun se oppgaven veldig kort før et gardin senkes foran oppgaven og de må svare. Etter at de har svart får de evaluert svaret sitt ved hjelp av enkelboksene. Det betyr at dette ikke er en vanlig quiz, men oppgaver der elevene lærer noe hvis de svarer feil. Årsaken til at oppgaven vises veldig kort før gardinen trekkes, handler om subitizing, og det å måtte forestille seg noe. Det står mer om dette under ”Lurt å vite” på denne siden. Subitizing er også temaet for den rike oppgaven denne uka.
Det siste av ukas mål handler om å tegne etter tabell. Hva det er, og forslag til hvordan dette kan introduserer for elevene, finner du i økt 3.
Gjennom to uker har vi nå beskrevet oppstart, egenaktiviteter og oppsummering av hver økt. Alle øktae (utenom de rike oppgavene) foregår på sammen måte:
- Oppstart i samling og utforsking. Utforskningen foregår enten i samling eller enkeltvis/i par av elever. Her brukes Mattesnakk-boka, øvingslabber, noomer eller annet konkretiseringsmateriale.
- Mengdetrening. Her er det egenaktiviteter på nettbrettet, i Mattestreker-boka og på kopiark.
- Oppsummering i samling.
Ønsket vårt er at lærere skal føle seg frie til å bruke verket vårt slik de selv synes er best. Vi har presentert våre tanker om bruka av det, og dere har sikkert egne ting dere gjerne vil ha med som ikke står beskrevet. Vi kommer derfor ikke til å fortsette med en detaljert beskrivelse av hver økt, men isteden bare liste opp målet med økta og alle tilgjengelige aktiviteter. Her finner du både videoer av øvingslabbene, sider fra bøkene og ting som kan printes ut. Vi anbefaler at minst halvparten av øktae brukes til utforskning.
For de som gjerne vil ha mer støtte, så er aktivitetene listet opp i den rekkefølgen vi tenker at de kan brukes. De gangene dette ikke er tilfelle, vil det stå beskrevet i teksten.
Nivåene i mengdetreningen er som følger:
- Grunnleggende: Den første siden med aktiviteter på nettbrettet og sidene i Mattesnakk-boka.
- Viderekommen: Den andre siden med aktiviteter på nettbrettet og kopiark.
- Avansert: Minispill og større spill i det som kalles ”free zone” på nettbrettet.
Det vil være noe flyt mellom nivåene: Enkelte steder vil kopiarkene fungere som ekstra trening for de som trenger det (for eksempel tallskriving). Det avanserte nivået kan alle elevene ha glede av å jobbe litt med, men det er også særlig beregnet for de som blir fort ferdig med alt og som trenger uendelig tilgang til ekstra aktiviteter.
Vi ønsker at du hver uke fortsette å lese teksten under Fokus og Lurt å vite. Her vil du finne veldig nyttig informasjon for undervisningspraksisen din.
Lurt å Vite
FORESTILLE SEG OG EVALUERE
Statped er opptatte av det de omtaler som ”dynamisk undervisning”. De trekker frem begrepet både når det er snakk om elever med matematikkvansker og i generell matematikkundervisning. Du kan lese mer om statped og dynamisk undervisning her i denne artikkelsamlingen, i kapittelet som heter ”Dynamisk undervisning”.
I veldig korte trekk dreier dynamisk undervisning seg om en dialogbasert tilnærming der den enkelte elev skal få mulighet til å_ forestille seg_ problemet og tenke gjennom det, gjerne deretter diskutere det med andre elever, for så å evaluere det de har kommet fram til. På denne måten får alle elevene mulighet til å både tenke og delta, og deretter få en vurdering av både tankerekken og strategien.
Vi har en utstrakt bruk av denne formen for undervisning i Dragonbox Skole. Så viktig mener vi at det er, at vi også har inkludert det i selve Dragonbox-metoden vår.
Hva betyr dette i praksis?
Vi ønsker at alle de felles utforsknings-aktivitetene har en ”forestille seg og evaluere”-tilnærming. Dette kan være øvingslabber, Mattesnakk-boka, de fysiske noomstavene, de rike oppgavene og andre felles utforskningsaktiviteter.
Hvis vi tar øvingslabbene som eksempel, så ønsker vi at når det er felles gjennomgang så skal denne utformes som en dialog mellom læreren og elevene, og ikke en monolog fra læreren som forteller elevene hva de skal lære. Dette kan foregå på følgende måte:
- Vi ønsker at alt som skal vises og læres starter med spørsmål som for eksempel ”Hva tror du skjer hvis...”.
- Gi nok tid for elevene til å_ forestille seg_ problemstillingen. Noen elever trenger også en påminnelse om at de nettopp må prøve å forestille seg hva som kommer til å skje.
- Elevene kan eventuelt snakke og diskutere sammen i par om hva de tenker.
- Til slutt kan noen av elevene eller parene få presentere løsningen sin, og når læreren så utfører oppgaven i øvingslabben, blir løsningen evaluert.
I forrige uke snakket vi litt om at øvingslabbene kan brukes på flere måter. Hvis man ønsker å bruke øvingslabben kun som en felles-aktivitet, så vil undervisningen bestå av mange små problemstillinger som elevene skal forestille seg, og hver ”forestille seg og evaluere”-runde tar bare ett minutts tid. Hvis man gir elevene en større problemstilling og lar elevene deretter utforske dette selv på nettbrettet sitt, så vil det ofte kun være én slik ”forestille seg og evaluere”-runde, og denne tar da lengre tid.
I de rike oppgavene er det også viktig med en ”forestille seg og evaluere”-tilnærming. Litt avhengig av oppgaven (for eksempel så har forrige ukes rike oppgave dette innebygget), så ønsker vi at alle oppgavene angripes først individuelt, deretter gjerne i par eller grupper, før man sammen ser på de ulike løsningsstrategiene og evaluerer dem. I boka Mattesnakk har vi lagt opp til at samtalen styres etter innspill fra elevene. De må da tenke gjennom hva de ser, før de forteller om tankene sine eller om hva de tror de skal lære av tegningene. Hjelpespørsmålene på sidene hjelper lærerne med å stille gode spørsmål til elevene når det trengs.
SUBITIZING
Som lærer møter vi stort sett hvert år de elevene som teller på fingrene når de regner. Vi tenker ikke da på de elevene som i oppgaven 4 + 3 tar opp 4 på den ene hånden, 3 på den andre hånden og sammen ser at dette blir 7. Vi tenker derimot på de elevene som i samme oppgave først teller opp 4 på hånden, fortsetter med å telle opp 3, og deretter teller hele mengden på nytt og får 7.
Denne telle-strategien gir en kortvarig glede. Den kan fungere gjennom 1. trinn, og ved å finpusse litt på strategien kan den også til dels fungere i 2. trinn. Men når man fortetter oppover i årene og skal lære om multiplikasjon, divisjon, brøk og desimaltall, så har elevene ingen hensiktsmessige strategier å bygge videre på. Ofte ser vi at disse elevene ender opp med alvorlige matematikkvansker.
Begrepet subitizing er kort fortalt evnen til å raskt kjenne igjen en mengde uten å telle den (*se kommentar nederst i teksten for utfyllende informasjon).
Forskning viser at barn har en medfødt evne til å skille mengder opp til 3 uten å telle. De kjenner altså igjen mengder som 1, 2, 3 eller mange. Denne evnen kan videreutvikles, slik at elevene kan lære seg å kjenne igjen også større mengder uten å telle. Elevene kjenner da igjen mengdene som tallbilder.
En terning er et godt eksempel på et tallbilde. Hver av de seks sidene har et fast mønster (et tallbilde), og etter å ha brukt terninger en stund kan de fleste elever kjenne igjen de 6 tallbildene på terningen uten å telle dem. Elevene kan også læres opp til å gjenkjenne mønster som for eksempel at en 2-er mengde og en 3-er mengde alltid blir 5. Når vi voksne kjenner igjen mengden 8 uten å telle den, så er det fordi hjernen automatisk sorterer gjenstandene til et tallbilde. Kanskje ser vi en 5’er og en 3’er, og dermed vet vi at vi har åtte. Kanskje finner vi to 4’ere. Uansett så skjer dette automatisk i hjernen, og når gjenstandene er plassert på en måte som ikke tillater slik sortering så klarer heller ikke vi å finne ut av hvor mange gjenstander det er uten å telle dem.
Som du kanskje har lagt merke til så er gjenkjennelse av tallbilder nært knyttet til forståelsen av helhet og deler som vi skrev litt om i ukestema 1. Og tallbildene er helt essensielle for å utvikle en god_ tallforstålse_.
Et godt eksempel er å kunne forstå tierovergang. De svake barna teller seg ofte oppover med fingrene, men det de trenger å forstå er at i oppgaven 8 + 5 så mangler 8 en 2’er for å bli en tier. De må også kjenne igjen at 5 kan deles i 2 og 3, og at mengden 10 og mengden 3 sammen blir 13.
Selve titallssystemet er også et godt eksempel på tallbilder fordi det bygges opp av gruppering i enere, tiere og så videre. For å forstå denne grupperingen må elevene ha forståelsen av deler og helhet. Vi skriver mer om helhet og deler når vi skal jobbe med tallvenner i ukestema 5.
Mange lærebøker_ motvirker gjenkjennelsen av tallbilder_ ved å bruke figurer som er komplekse og der gjenstandene er plassert uten system. Dette gjør at det blir umulig å gruppere gjenstandene, og dermed blir telling den eneste mulige strategien. I Dragonbox Skole har vi derimot et stort fokus på dette, og gjennomgående for hele læreverket er at vi ”sorterer” gjenstandene i mønster elevene skal kunne kjenne igjen. Vi vender også stadig tilbake til hensiktsmessige modeller som enkelboksen, hvor det røde og de to blå merkene hjelper elevene til å forstå mengdene som deler og helhet istedenfor å telle seg oppover. På denne måten får elevene mulighet til å utvikle en bedre og rikere tallforståelse.
UTFYLLENDE KOMMENTAR TIL TEKSTEN OVER:
I teksten over har vi prøvd å gi en kortfattet og enkel oppsummering av hvordan subitizing henger sammen med det vi gjør i læreverket. Begrepet subitizing ble antagelig første gang nevnt i forskning i 1949, men selve forskningen på fenomenet går lengre tilbake. Mye forskning på et emne fører ofte til motstridene resultater, og slik er det også med subitizing. Forskerne har for eksempel ulike teorier om hvilke mengder som kan kjennes igjen og hvor fort barna kan kjenne dem igjen. Begrepet subitizing brukes også ulikt: Noen bruker det utelukkende om den første forståelsen av mengdene opp til 3, mens andre bruker det om forståelsen av tallbilder. I forskningen omtales av og til den medfødte evnen til å kunne gjenkjenne et antall som perseptuell subitizing. Det betyr at de små barna kjenner igjen mengdene uten bruk av innlært matematisk kunnskap som for eksempel telling. Den videreutviklede evnen til å gjenkjenne tallbilder med større mengder omtales av og til som_ konseptuell subitizing_. Det betyr at barna gjenkjenner et tallbilde som bestående av både deler og en helhet. For eksempel så kan eleven kjenne igjen de to delmengdene 3, og da vite at helheten er 6.
Hjemmelekse
Vårt forslag til lekser denne uka er å fortsette med matematikk-dialog mellom elever og foreldre. I boka Mattesnakk er sidene 12 – 21 (de fem første tallene) fine å gi som lekser denne uka.
Økt 1: Repetisjon: enkelboksen og tallskriving
Mål
Elevene skal kunne:
- Tegne og gjenkjenne mengder opp til 5 med støtte i modell (enkelboks).
- Skrive tallene 1-5 med hjelpelinje.
Ekstra utstyr
Fokus
Beskrivelse
Dette er en repetisjonsøkt, så de fleste elevene er allerede kjent med det de skal jobbe med denne økta. Det gir en god anledning til å la elevene forklare for klassen eller for hverandre i par hvordan tallene skrives og hvor høyt opp ulike mengder når opp i enkelboksen.
Vær oppmerksom på at elevene skal bruke det første blå og det røde merket i enkelboksen for å beskrive hvor høyt mengdene kommer.
Økt 2: Ulike tallrepresentasjoner
Mål
Elevene skal kunne:
- Representere mengder under 5 på forskjellige måter (tall, noomer, enkelbokser, terninger, fingre).
Ekstra utstyr
Fokus
Beskrivelse
I tillegg til øvingslab-videoen som du finner til høyre på denne sida, så er et tips til denne økta å bruke litt utforskningstid på å finne ulike mengder i klasserommet eller ute. Kan elevene finne 4’er mengder i klasserommet? Kan de finne 5’er mengder? Hvordan kan man vite at det er 5 uten å telle dem?
Vi oppfordrer også sterkt til å huske på dette med å forestille seg og verifisere som bekrevet under ”Lurt å vite” på ukestema-sida. Prøv så langt det lar seg gjøre å ikke fortelle elevene om hva som skjer og hvordan de skal tenke. La istedet undervisningen bestå av gode spørsmål til elevene. Be dem forestille seg det som skjer og evaluer deretter svarene deres.
TIPS: Lag gjerne en konkurranse med deg selv om hvor mange gode spørsmål du klarer å stille elevene i løpet av en økt.
Økt 3: Tallskriving og tegne etter tabell
Mål
Elevene skal kunne:
- Lese av enkel tabell.
- Skrive tallene 0-5 med hjelpelinje.
Ekstra utstyr
Flere blanke ark til hver elev.
Fokus
Beskrivelse
For at elevene skal kunne jobbe i Mattestrekker denne økta, må de først introduseres for tabell. Her er et forslag til en slik introduksjon:
Tegn en figur på tavla og en tabell med to kolonner og én rad med et hode, som på dette bildet:
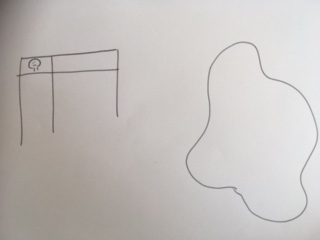
Spør elevene: Hvor mange hoder skal monsteret vårt ha? Bruk et av svarene som er mindre enn 4. Tegn dette inn i tabellen og på tegningen, for eksempel som dette:
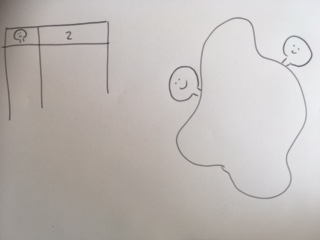
Tegn en rad med føtter og spør elevene: Hvor mange føtter skal monsteret vårt ha? Bruk et av svarene som er mindre enn 4.
Tegn en rad med armer og spør: Hvor mange armer skal monsteret vårt ha? Fortett slik til hode, bein, armer, hatter og så videre er tegnet inn. Da kan det for eksempel se noe slikt ut:
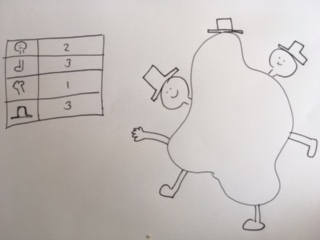
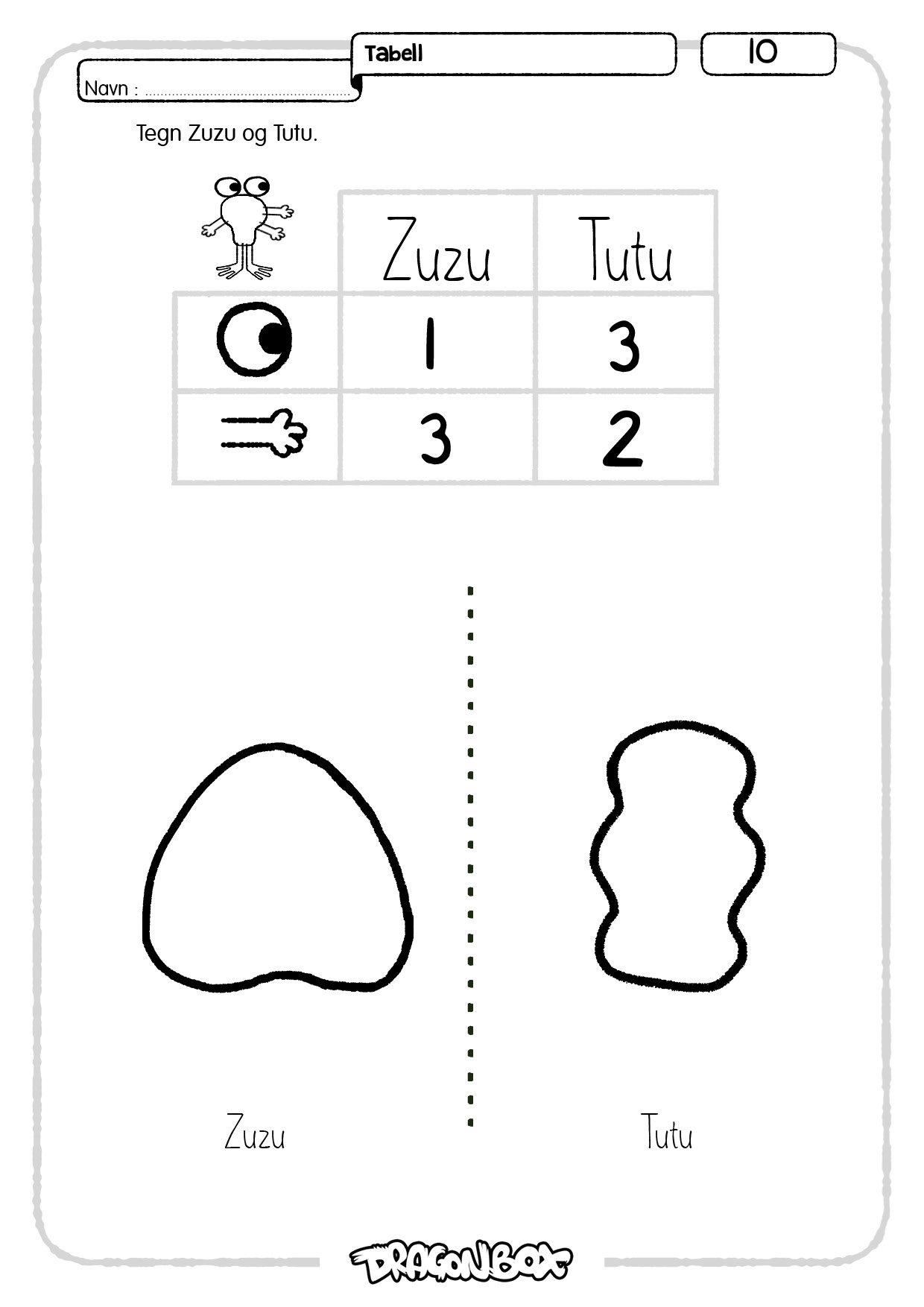
La alle elevene få ett ark hver og be dem tegne en sirkel på arket. Tegn en tabell på tavla som inneholder munn, øyne, øre, tenner, hatt og andre ting du kan komme på. Bildet under er et eksempel:
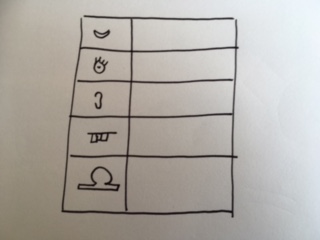
Ta opp noen elever og la dem fylle inn tabellen sammen med deg.
La alle elevene fylle inn detaljer på sirklene sine slik at de stemmer overens med tabellen.
Ta opp noen elever og la dem få vise hva de har tegnet.
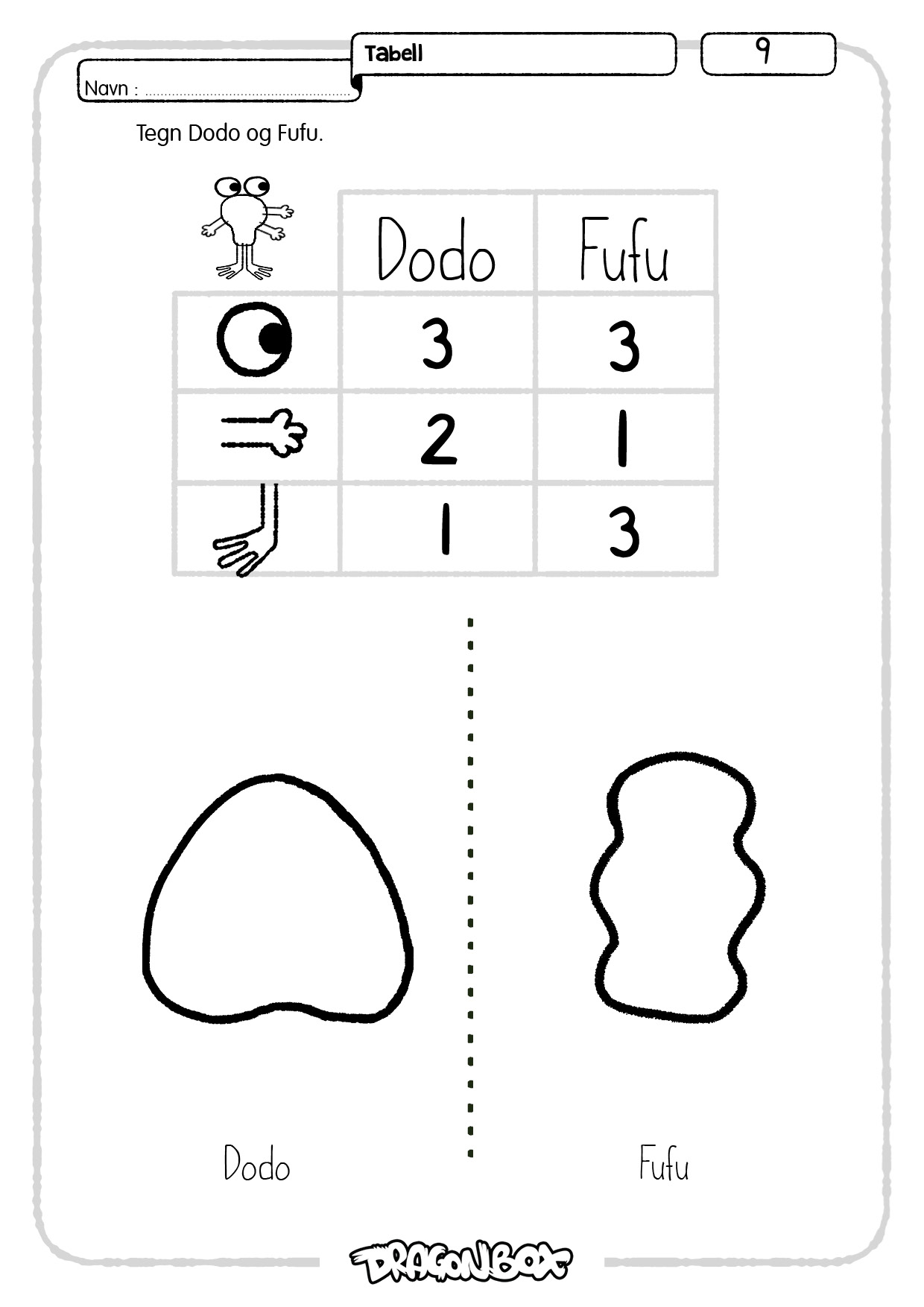
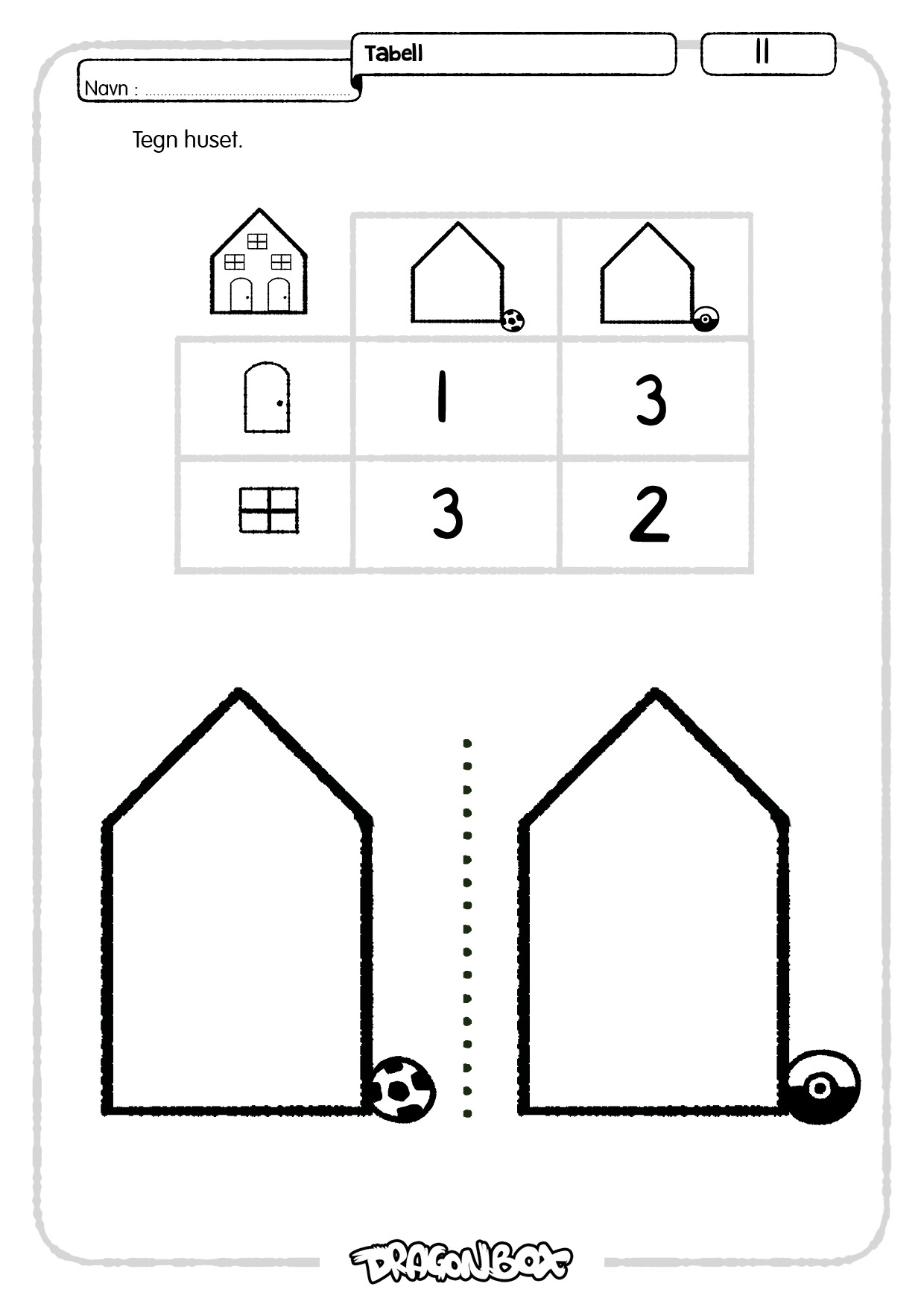
Tegn nå to figurer og en tabell med 3 kolonner og 4 rader, slik som på dette bildet:
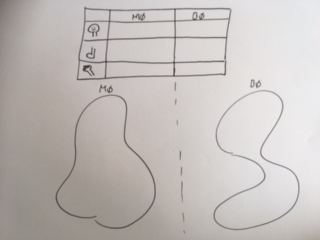
Spør elevene: Hvor mange hoder skal hvert av disse monstrene ha? Velg blant svarene til elevene slik at tallene ikke blir høyere enn 5 og slik at de to monstrene får forskjellig antall hoder. Be to elever komme opp for å tegne inn hodene på figurene. Er de andre elevene enige?
Be elever komme opp for å fylle in tabellen og deretter tegne inn armer og bein. Spør hele tiden om de andre elevene er enige eller har andre forslag.
Fortsett med oppgaver til elevene mestrer dette. La dem så få prøve på egenhånd i Mattestreker. Når de er ferdige med Mattestreker så kan de jobbe i par: Den ene lager en tabell og den andre lager en fantasi-figur. Nå skal den andre bruke tabellen til fylle armer, ben med mer inn i fantasifiguren sin. Deretter bytter de roller.
Økt 4: Rik oppgave: Subitizing-spill
Mål
Øve på å kjenne igjen tallbilder (subitizing).
Ekstra utstyr
- Spillbrettene som ligger til høyre på denne sida. Vi anbefaler å printe 4 eller 6 stk av hvert brett og deretter laminere dem slik at de kan brukes flere ganger.
- 1 terning til hvert par av elever.
Fokus
Beskrivelse
Her kommer først er kort beskrivelse. For en utfyllende beskrivelse klikk i den gule boksen til høyre.
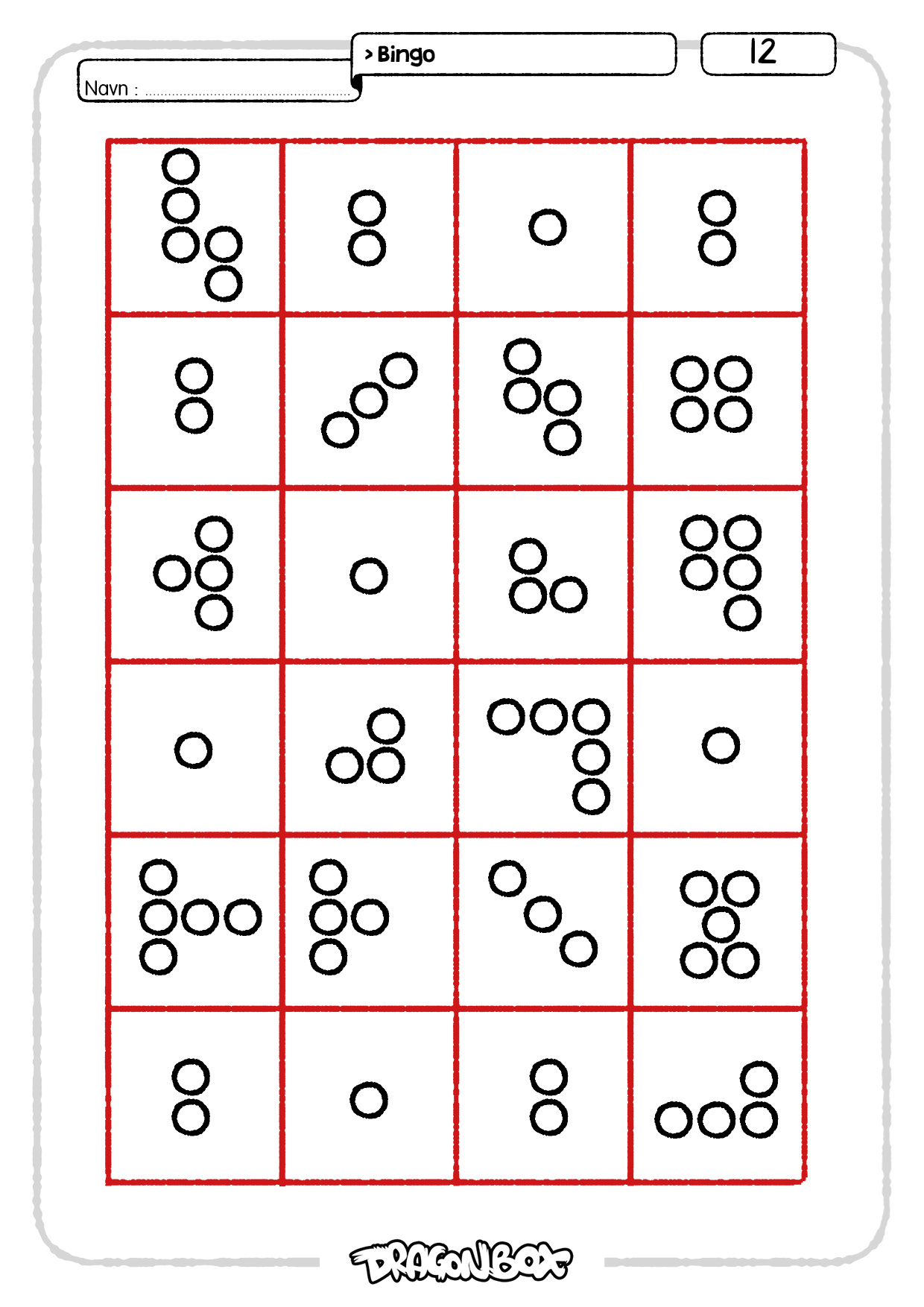
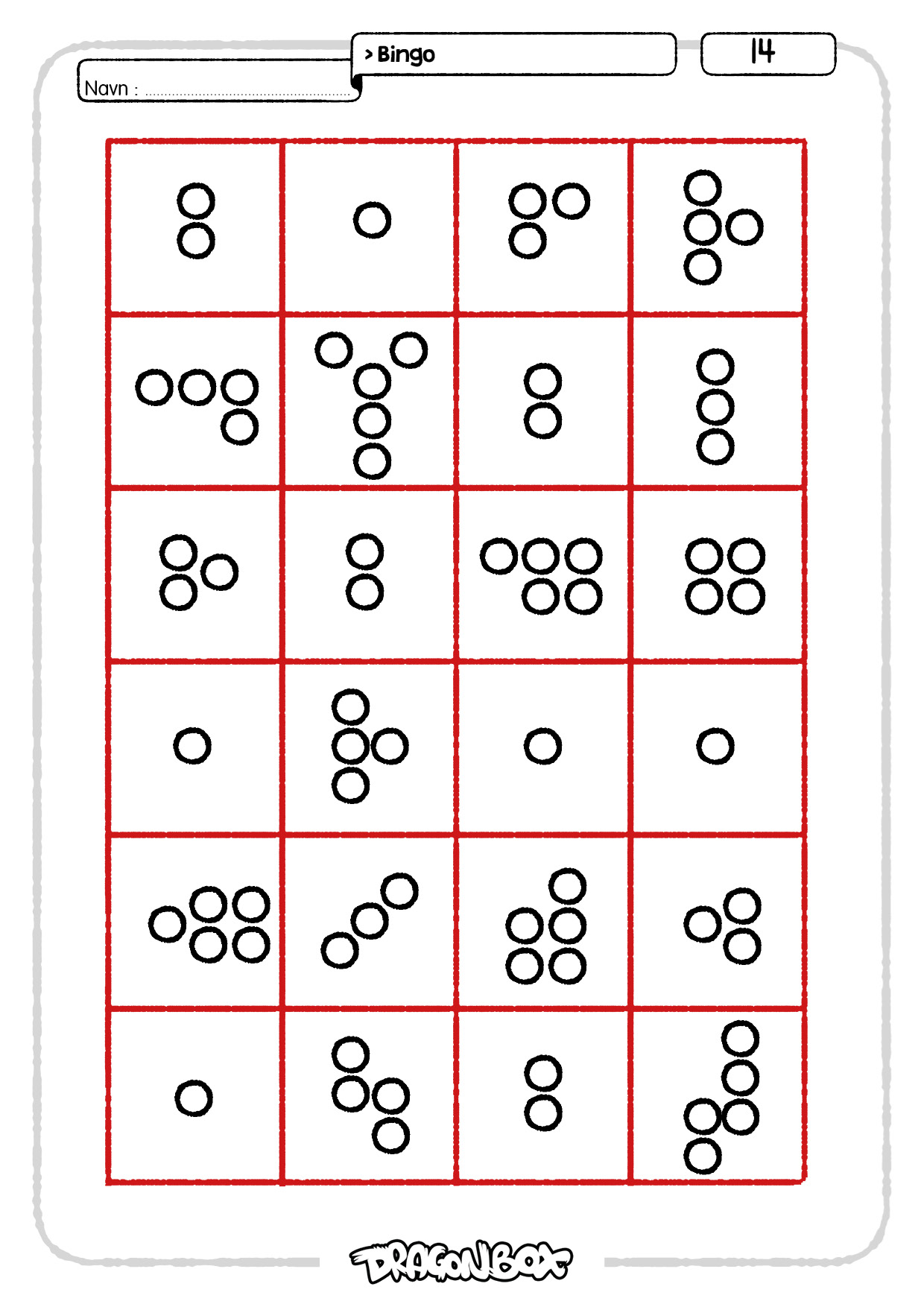
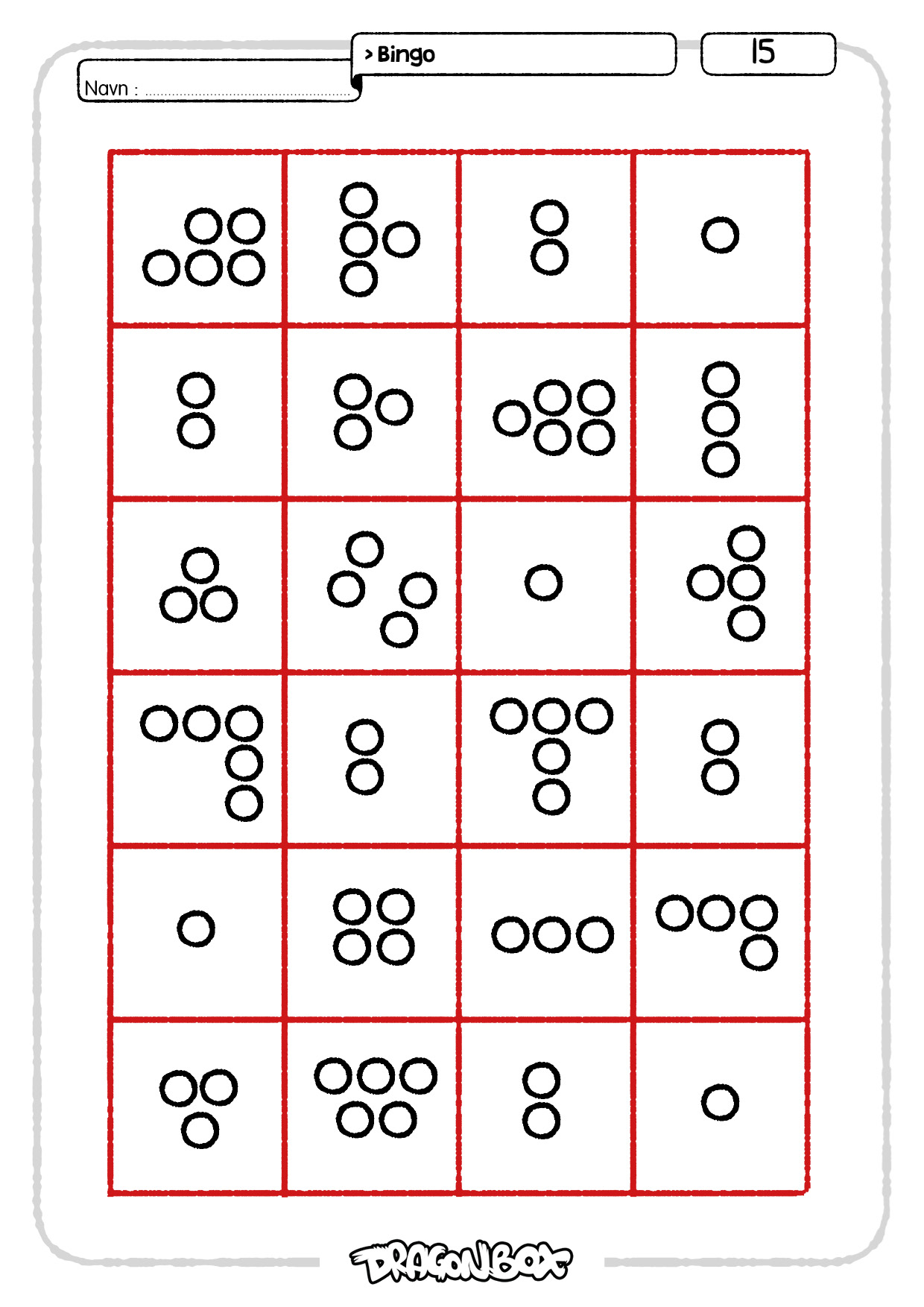
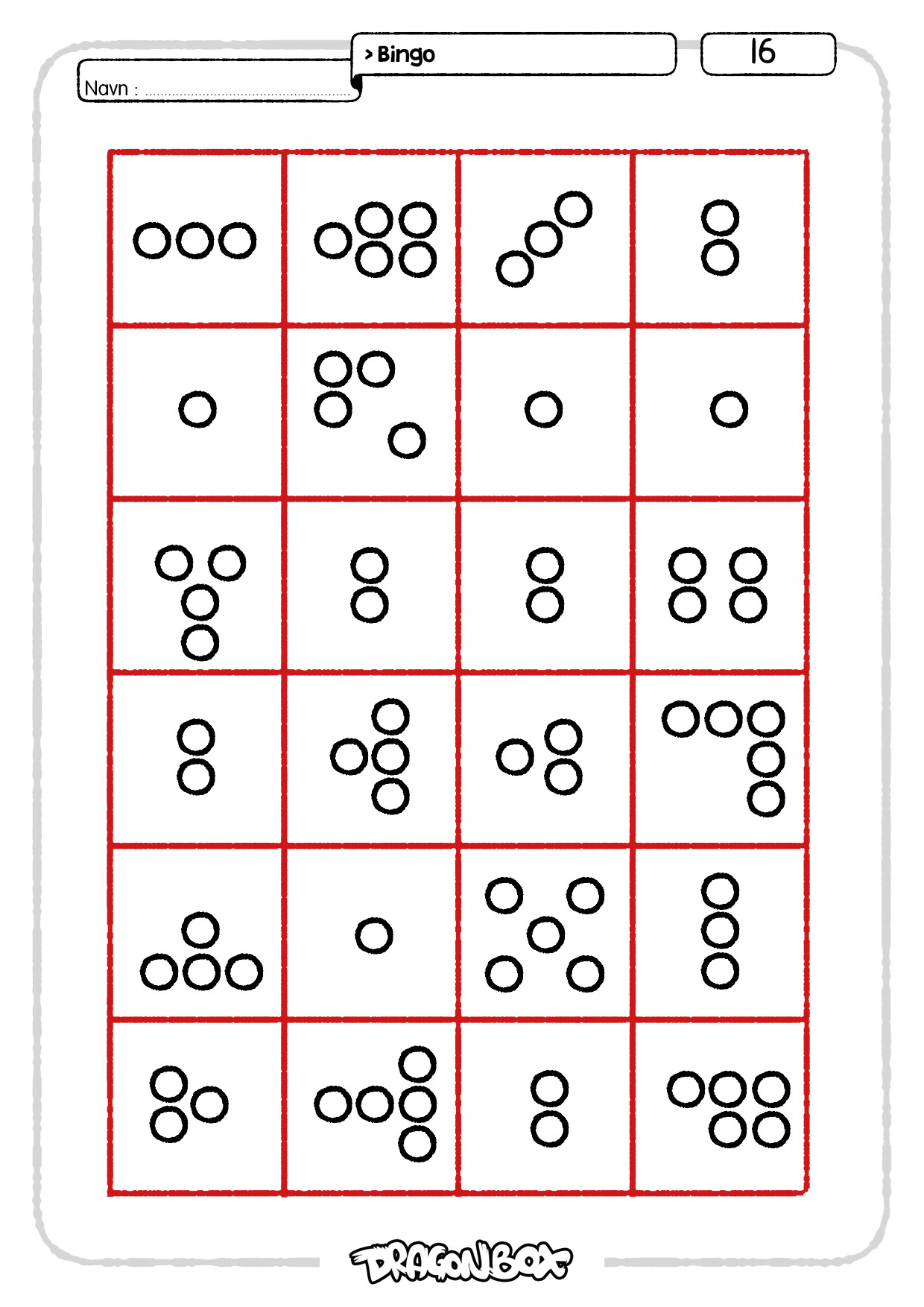
Spillbrettene inneholder 24 felter med mengder fra 1 til 5. Målet er at elevene skal bli vant med å raskt kjenne igjen disse mengdene uten å telle dem.
Spillbrettene kan brukes på mange forskjellige måter. Et mål kan være å krysse ut gitte mengder. Man kan bruke terninger, rope opp tall, vise tallkort og lignende for å velge hvilke mengder som skal krysses ut. Elevene kan også telle hvor mange de har av hver mengde på brettet sitt. Er tallet likt som på brettene til de andre elevene?
TIPS: Ved å laminere spillbrettene og bruke tusjer som kan vaskes vekk fra plastikk (de fleste tusjer kan det), så kan spillbrettene brukes mange ganger. Alternativt kan man legge en stein, en lapp eller noe annet over de feltene som skal ”krysses ut”.
 Rik oppgave: Subitizing-spill
Rik oppgave: Subitizing-spill
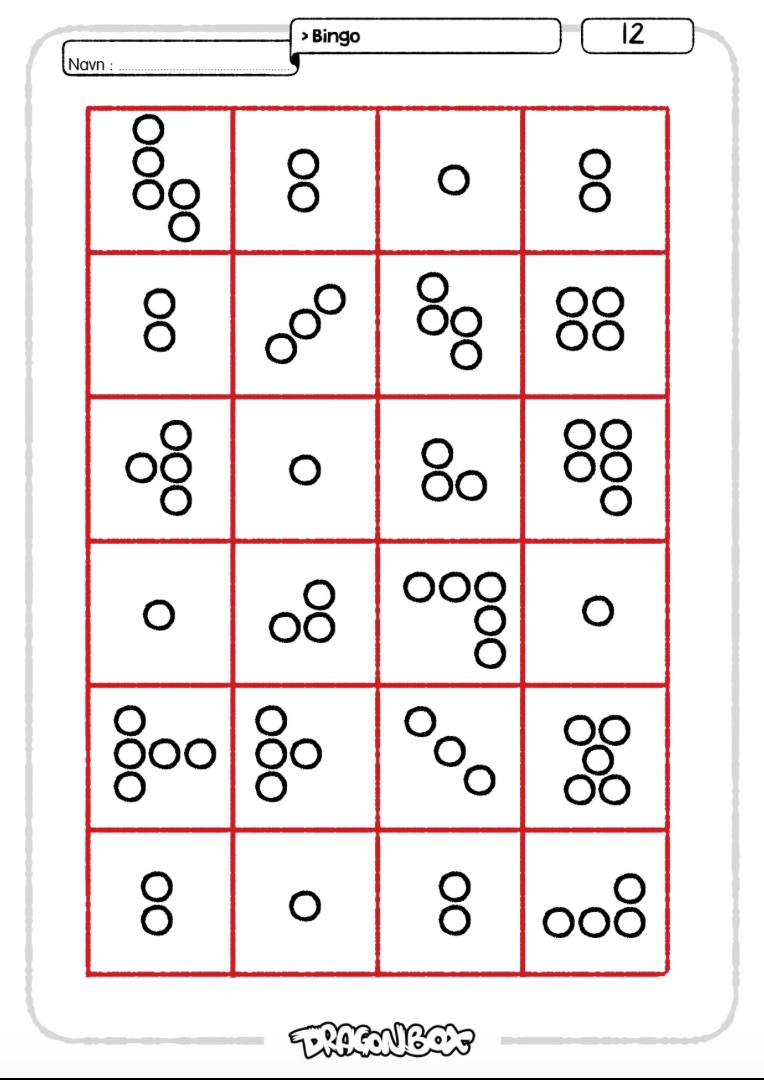

Her kommer 3 forslag til spill som man kan bruke subitizing-brettene til.
Subitizing-spill med terning:
Del elevene inn i par. Alle elevene får hvert sitt spillbrett, men begge spillbrettene i et par skal være like. Så hvis Per og Pål er et par, så har begge to helt likt spillbrett. Hvert par får en terning hver. Den ene i paret begynner å kaste terningen, og neste gang er det den andre siden tur. Slik fortsetter det til spillet er over. Når en elev kaster terningen så skal den prøve å finne en mengde på sitt brett som tilsvarer mengden på terningen. La oss si at Per kaster 5. Da må han prøve å finne en 5’er mengde på sitt brett. Hvis han finner en slik så krysser han den ut. Hvis han ikke finner mengden eller ikke har flere 5’er mengder igjen så er det Pål sin tur. Den første som har krysset ut alle mengdene på brettet sitt (fullt brett) vinner. NB: Det er ingen 6’er mengde på brettene, så elevene vil oppdage at det ikke er så gøy å få 6 på terningen, i motsetning til mange andre spill.
Subitizing-spill styrt av læreren:
La elevene få hvert sitt brett. Rop opp et tall mellom 1 og 5. Etter noen sekunder roper du opp neste tall. Det er nå om å gjøre for elevene å finne en mengde som passer før neste tall ropes opp. Fortell elevene at de må lete så fort som mulig, for etter noen sekunder går man videre til neste tall. Den som først får fylt sitt brett vinner. Stopp gjerne opp underveis for å få tips fra elevene til hvordan man raskt kan finne mengden man leter etter. TIPS: Denne oppgaven kan selvfølgelig gjøres på mange måter. Kast en terning, vis tallkort slik at elevene blir vant med å assosiere selve tallene til mengder eller kom på andre gøye måter å organisere spillet på.
Subitizing-spill ute i naturen:
La elevene gå ut i naturen for å lete etter mengder som de så krysser av på brettet sitt. En annen variant kan være å samle mengder slik at de til slutt har alle mengdene som er på brettet. Den siste varianten er mer krevende, fordi elevene må holde oversikt over hvilke mengder de har funnet og ikke.